Advertisements
Advertisements
Question
ABCD is a parallelogram in which diagonal AC bisects ∠BAD. If ∠BAC = 35°, then ∠ABC =
Options
70°
110°
90°
120°
Solution
ABCD is a parallelogram in which AC bisects ∠A.
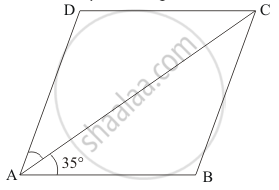
It is given that ∠BAC = 35°
Therefore,
∠BAD = 2(∠BAC)
∠BAD = 2(35°)
∠BAD = 70°
Since, DC || AB
Therefore,
∠BAD + ∠ABC = 180°
70° +∠ABC = 180°
∠ABC = 110°
Hence, the correct choice is (b).
APPEARS IN
RELATED QUESTIONS
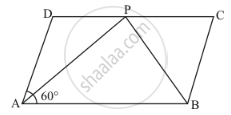
In Fig., below, ABCD is a parallelogram in which ∠A = 60°. If the bisectors of ∠A and ∠B meet at P, prove that AD = DP, PC = BC and DC = 2AD.
In a parallelogram ABCD, determine the sum of angles ∠C and ∠D .
The sides AB and CD of a parallelogram ABCD are bisected at E and F. Prove that EBFD is a parallelogram.
In a ΔABC median AD is produced to X such that AD = DX. Prove that ABXC is a
parallelogram.
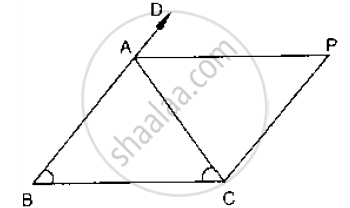
In Fig. below, AB = AC and CP || BA and AP is the bisector of exterior ∠CAD of ΔABC.
Prove that (i) ∠PAC = ∠BCA (ii) ABCP is a parallelogram
In a parallelogram ABCD, if ∠A = (3x − 20)°, ∠B = (y + 15)°, ∠C = (x + 40)°, then find the values of xand y.
In a parallelogram ABCD, the bisector of ∠A also bisects BC at X. Find AB : AD.
The figure formed by joining the mid-points of the adjacent sides of a rhombus is a
In the given figure, ∠A = 64°, ∠ABC = 58°. If BO and CO are the bisectors of ∠ABC and ∠ACB respectively of ΔABC, find x° and y°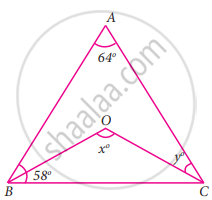
In the given Figure, if AB = 2, BC = 6, AE = 6, BF = 8, CE = 7, and CF = 7, compute the ratio of the area of quadrilateral ABDE to the area of ΔCDF. (Use congruent property of triangles)
