Advertisements
Advertisements
Question
If the diagonals of a rhombus are 18 cm and 24 cm respectively, then its side is equal to
Options
16 cm
15 cm
20 cm
17 cm
Solution
Let ABCD be rhombus with diagonals AC and BD 18cm and 24cm respectively.
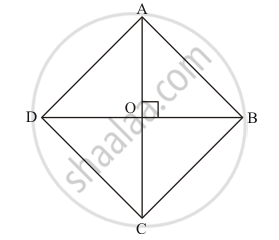
We know that diagonals of the rhombus bisect each other at right angles.
Therefore,
`AO = 1/2 AC `
`AO = 1/2 (18cm) `
AO = 9cm
Similarly,
`BO = 1/2 BD `
`BO = 1/2(24cm)`
BO = 12cm
Also, ΔAOB is a right angled triangle.
By Pythagoras theorem, we get:
`AB^2 = AO^2 + BO^2`
`AB = sqrt(AO^2 + BO^2)`
`AB = sqrt(9^2 + 12^2)`
`AB = sqrt225`
AB = 15cm
Hence the correct choice is (b).
APPEARS IN
RELATED QUESTIONS
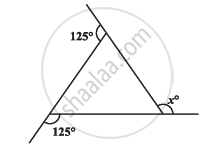
Find x in the following figure:
ABCD is a parallelogram in which ∠A = 70°. Compute ∠B, ∠C and ∠D .
In the given figure, ABCD is a rectangle in which diagonal AC is produced to E. If ∠ECD = 146°, find ∠AOB.
If an angle of a parallelogram is two-third of its adjacent angle, the smallest angle of the parallelogram is
In ΔABC, ∠A = 30°, ∠B = 40° and ∠C = 110°. The angles of the triangle formed by joining the mid-points of the sides of this triangle are
The angle between two altitudes of a parallelogram through the vertex of an obtuse angle of the parallelogram is 60º. Find the angles of the parallelogram.
In the following figure, P is the mid-point of side BC of a parallelogram ABCD such that ∠BAP = ∠DAP. Prove that AD = 2CD.

A quadrilateral has three acute angles. If each measures 80°, then the measure of the fourth angle is ______.
The sum of all ______ of a quadrilateral is 360°.
Sum of all the angles of a quadrilateral is 180°.
