Advertisements
Advertisements
Question
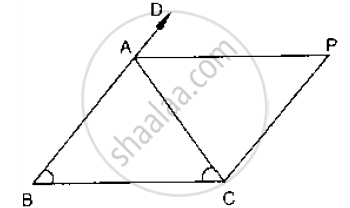
In Fig. below, AB = AC and CP || BA and AP is the bisector of exterior ∠CAD of ΔABC.
Prove that (i) ∠PAC = ∠BCA (ii) ABCP is a parallelogram
Solution

Given
AB = AC and CD || BA and AP is the bisector of exterior
∠CAD of ΔABC
To prove:
i) ∠PAC = ∠BCA
ii) ABCP is a parallelogram
Proof:
i) We have,
AB = AC
⟹ ∠ACB = ∠ABC [Opposite angles of equal sides of triangle are equal]
Now, ∠CAD = ∠ABC + ∠ACB
⇒ ∠PAC + ∠PAD = 2∠ACB (∵ ∠PAC = ∠PAD )
⇒ 2∠PAC = 2∠ACB
⇒ ∠PAC = ∠ACB
ii) Now,
∠PAC = ∠BCA
⇒ AP || BC
And, CP || BA [Given]
∴ ABCP is a parallelogram .
APPEARS IN
RELATED QUESTIONS
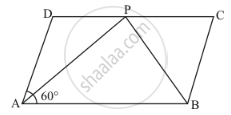
In Fig., below, ABCD is a parallelogram in which ∠A = 60°. If the bisectors of ∠A and ∠B meet at P, prove that AD = DP, PC = BC and DC = 2AD.
In a parallelogram ABCD, determine the sum of angles ∠C and ∠D .
In a parallelogram ABCD, if `∠`B = 135°, determine the measures of its other angles .
ABCD is a square. AC and BD intersect at O. State the measure of ∠AOB.
The sides AB and CD of a parallelogram ABCD are bisected at E and F. Prove that EBFD is a parallelogram.
P and Q are the points of trisection of the diagonal BD of a parallelogram AB Prove that CQ is parallel to AP. Prove also that AC bisects PQ.
In a parallelogram ABCD, if ∠D = 115°, then write the measure of ∠A.
PQRS is a quadrilateral, PR and QS intersect each other at O. In which of the following case, PQRS is a parallelogram?
∠P = 100°, ∠Q = 80°, ∠R = 95°
We get a rhombus by joining the mid-points of the sides of a
P is the mid-point of side BC of a parallelogram ABCD such that ∠BAP = ∠DAP. If AD = 10 cm, then CD =
