Advertisements
Advertisements
Question
P is the mid-point of side BC of a parallelogram ABCD such that ∠BAP = ∠DAP. If AD = 10 cm, then CD =
Options
5 cm
6 cm
8 cm
10 cm
Solution
Parallelogram ABCD is given such that ∠BAP = ∠DAP
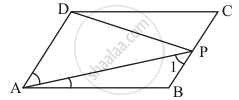
We haveAD = 10cm and `BC = 1/2 BC`
We need to find the measure of side CD.
Since BC || AD and AP as transversal
∠I = ∠DAP
But it is given that
∠BAP = ∠DAP
Therefore, we get:
∠I = ∠BAP
Also, sides opposite to equal angles are equal.
Then,
AB = BP …… (I)
Also, `BP = 1/2 BC`
Substituting`BP = 1/2 BC`in (I), We get:
`AB = 1/2 BC`
It is given that AD = 10cm, this means opposite side BC = 10cm,asABCD is a parallelogram. Therefore,
`AB = 1/2 (10cm)`
AB = 5cm
Or, CD = 5cm
Hence the correct choice is (a).
APPEARS IN
RELATED QUESTIONS
In a parallelogram ABCD, determine the sum of angles ∠C and ∠D .
P and Q are the points of trisection of the diagonal BD of a parallelogram AB Prove that CQ is parallel to AP. Prove also that AC bisects PQ.
In a ΔABC median AD is produced to X such that AD = DX. Prove that ABXC is a
parallelogram.
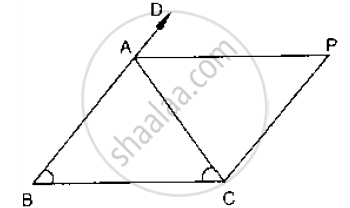
In Fig. below, AB = AC and CP || BA and AP is the bisector of exterior ∠CAD of ΔABC.
Prove that (i) ∠PAC = ∠BCA (ii) ABCP is a parallelogram
In a parallelogram ABCD, if ∠D = 115°, then write the measure of ∠A.
In a parallelogram ABCD, the bisector of ∠A also bisects BC at X. Find AB : AD.
We get a rhombus by joining the mid-points of the sides of a
In the given figure, ∠A = 64°, ∠ABC = 58°. If BO and CO are the bisectors of ∠ABC and ∠ACB respectively of ΔABC, find x° and y°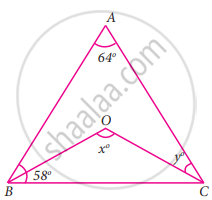
ABCD is a square, diagonals AC and BD meet at O. The number of pairs of congruent triangles with vertex O are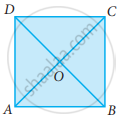
Prove that the quadrilateral formed by the bisectors of the angles of a parallelogram is a rectangle.
