Advertisements
Advertisements
Question
In ΔABC, E is the mid-point of median AD such that BE produced meets AC at F. IF AC = 10.5 cm, then AF =
Options
3 cm
3.5 cm
2.5 cm
5 cm
Solution
ΔABC is given with E as the mid-point of median AD.
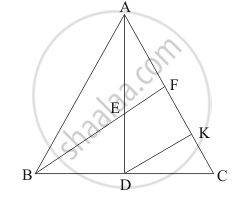
Also, BE produced meets AC at F.
We have AC = 10. 5cm , then we need to find AF.
Through D draw DK || BF.
In ΔADK, E is the mid-point of AD and EF || DK.
Using the converse of mid-point theorem, we get:
AF = FK…… (i)
In ,ΔBCFD is the mid-point of BC and BF || DK.
KC = FK…… (ii)
From (i) and (ii),we have:
AF = FK , AF = KC…… (iii)
Now,
AC = AF +FK + KC
AC = AF + FK + KC
From (iii) equation, we get:
AC = AF + AF + AF
AC = 3AF
` AF = 1/3 AC` …… (iv)
We have AC = 10.5cm .Putting this in equation (iv), we get:
`AF = 1/3(10.5cm)`
AF = 3.5cm
Hence the correct choice is (b).
APPEARS IN
RELATED QUESTIONS
Complete of the following, so as to make a true statement:
The number of pairs of opposite angles of a quadrilateral is .......
Complete of the following, so as to make a true statement:
In a quadrilateral the point of intersection of the diagonals lies in .... of the quadrilateral.
In a quadrilateral ABCD, CO and DO are the bisectors of ∠C and ∠D respectively. Prove that \[∠COD = \frac{1}{2}(∠A + ∠B) .\]
In quadrilateral ABCD, side AB is parallel to side DC. If ∠A : ∠D = 1 : 2 and ∠C : ∠B = 4 : 5
(i) Calculate each angle of the quadrilateral.
(ii) Assign a special name to quadrilateral ABCD
If three angles of a quadrilateral are 90° each, show that the given quadrilateral is a rectangle.
The angles of a pentagon are x°, (x - 10)°, (x + 20)°, (2x - 44)° and (2x - 70)°. Find the angles.
If bisectors of ∠A and ∠B of a quadrilateral ABCD intersect each other at P, of ∠B and ∠C at Q, of ∠C and ∠D at R and of ∠D and ∠A at S, then PQRS is a ______.
If APB and CQD are two parallel lines, then the bisectors of the angles APQ, BPQ, CQP and PQD form ______.
In given figure, What is BD – BE?
Can we have two obtuse angles whose sum is a complete angle? Why or why not?
