Question

ABCD is a parallelogram and E is the mid-point of BC. DE and AB when produced meet at F. Then, AF =

Options

• \[\frac{3}{2}AB\]

• 2 AB

• 3 AB

• \[\frac{5}{4}AB\]

Answer 1

Parallelogram ABCD is given with E as the mid-point of BC.

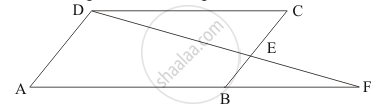
DE and AB when produced meet at F

We need to find AF.

Since ABCD is a parallelogram, then DC || AB

Therefore, DC || AF

Then, the alternate interior angles should be equal.

Thus, ∠DCE = ∠CBF …… (I)

In ΔDEC and ΔFEB:

∠DEC = ∠CBF (From(I))

CE = BE (E is the mid-point of BC)

∠CED = ∠BEF  (Vertically opposite angles)

 ΔDEC ≅ ΔFEB (by ASA Congruence property)

We know that the corresponding angles of congruent triangles should be equal.

Therefore,

DC = BF

But,

DC = AB  (Opposite sides of a parallelogram are equal)

Therefore,

BF = AB …… (II)

Now,

AF = BF + AB

From (II),we get:

AF = AB +AB

AF = 2AB

Hence the correct choice is (b).