Advertisements
Advertisements
Question
The bisectors of any two adjacent angles of a parallelogram intersect at
Options
30°
45°
60°
90°
Solution
Let the figure be as follows:
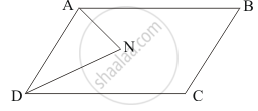
ABCD is a parallelogram.
We have to find ∠DNA
AN and AD is the bisectors of ∠A and ∠D.
Therefore,
`∠DAN = 1/2 ∠A` …… (i)
And
`∠ADN = 1/2 ∠D` …… (ii)
We know that AB || DC.
Therefore, the sum of consecutive interior angles must be supplementary.
`∠A + ∠D = 180°`
`1/2∠A + 1/2∠D = 180°/2`
From (i) and (ii), we get
∠DAN + ∠ADN = 90°…… (iii)
By angle sum property of a triangle:
∠DAN + ∠DAN + ∠ADN = 180°
∠DNA + 90° = 180°
∠DNA = 180° - 90°
∠DNA = 90°
Hence the correct choice is (d).
APPEARS IN
RELATED QUESTIONS
Show that if the diagonals of a quadrilateral bisect each other at right angles, then it is a rhombus.
Show that if the diagonals of a quadrilateral are equal and bisect each other at right angles, then it is a square.
ABCD is a rhombus. Show that diagonal AC bisects ∠A as well as ∠C and diagonal BD bisects ∠B as well as ∠D.
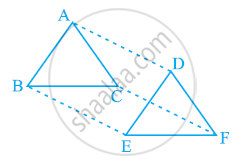
In ΔABC and ΔDEF, AB = DE, AB || DE, BC = EF and BC || EF. Vertices A, B and C are joined to vertices D, E and F respectively (see the given figure). Show that
(i) Quadrilateral ABED is a parallelogram
(ii) Quadrilateral BEFC is a parallelogram
(iii) AD || CF and AD = CF
(iv) Quadrilateral ACFD is a parallelogram
(v) AC = DF
(vi) ΔABC ≅ ΔDEF.
The following statement are true and false .
In a parallelogram, the diagonals are equal
In the given figure, ABCD and AEFG are two parallelograms. If ∠C = 58°, find ∠F.
PQRS is a quadrilateral, PR and QS intersect each other at O. In which of the following case, PQRS is a parallelogram?
PQ = 7 cm, QR = 7 cm, RS = 8 cm, SP = 8 cm
The bisectors of the angle of a parallelogram enclose a
The diagonals of a parallelogram ABCD intersect at O. If ∠BOC = 90° and ∠BDC = 50°, then ∠OAB =
ABCD is a parallelogram and E is the mid-point of BC. DE and AB when produced meet at F. Then, AF =
