Advertisements
Advertisements
Question
In a rhombus ABCD, if ∠ACB = 40°, then ∠ADB =
Options
70°
45°
50°
60°
Solution
Rhombus ABCD is given as follows:
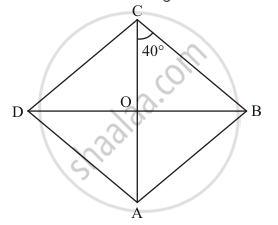
It is given that∠ACB = 40°.
Therefore, ∠OCB = 40° (Because O lies on AC)
We know that the diagonals of a rhombus intersect at right angle.
Therefore, ∠BOC = 90°
By angle sum property of a triangle, we get:
∠CBO + ∠OCB + ∠BOC = 180°
∠CBO + 40° + 90° = 180°
∠CBO+ 130° = 180 °
∠CBO = 50°
Since, O lies on BD
∠CBD = 50°
Also , CB || DA
Therefore,
∠ADB = ∠CBD
∠ADB = 50°
Hence, the correct choice is (c).
APPEARS IN
RELATED QUESTIONS
In a quadrilateral ABCD, the angles A, B, C and D are in the ratio 1 : 2 : 4 : 5. Find the measure of each angles of the quadrilateral
The diagonals of a rectangle ABCD meet at O, If ∠BOC = 44°, find ∠OAD.
In the given figure, PQRS is a rhombus in which the diagonal PR is produced to T. If ∠SRT = 152°, find x, y and z.

In the given figure, ABCD is a rectangle in which diagonal AC is produced to E. If ∠ECD = 146°, find ∠AOB.
The two diagonals are equal in a
Can the angles 110º, 80º, 70º and 95º be the angles of a quadrilateral? Why or why not?
Can all the angles of a quadrilateral be acute angles? Give reason for your answer.
One angle of a quadrilateral is of 108º and the remaining three angles are equal. Find each of the three equal angles.
In the following figure, P is the mid-point of side BC of a parallelogram ABCD such that ∠BAP = ∠DAP. Prove that AD = 2CD.

The angles P, Q, R and S of a quadrilateral are in the ratio 1:3:7:9. Then PQRS is a ______.
