Advertisements
Advertisements
Question
In a parallelogram ABCD, write the sum of angles A and B.
Solution
In Parallelogram ABCD, ∠A and ∠Bare adjacent angles.
Thus, AB || DC
Then, we have ∠A and ∠B as consecutive interior angles which must be supplementary.
∠A + ∠B = 180°
Hence, the sum of ∠A and ∠B is 180°.
APPEARS IN
RELATED QUESTIONS
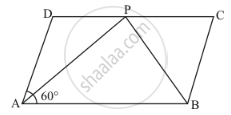
In Fig., below, ABCD is a parallelogram in which ∠A = 60°. If the bisectors of ∠A and ∠B meet at P, prove that AD = DP, PC = BC and DC = 2AD.
In a parallelogram ABCD, if `∠`B = 135°, determine the measures of its other angles .
In a parallelogram ABCD, if ∠A = (3x − 20)°, ∠B = (y + 15)°, ∠C = (x + 40)°, then find the values of xand y.
We get a rhombus by joining the mid-points of the sides of a
The figure formed by joining the mid-points of the adjacent sides of a parallelogram is a
ABCD is a parallelogram in which diagonal AC bisects ∠BAD. If ∠BAC = 35°, then ∠ABC =
P is the mid-point of side BC of a parallelogram ABCD such that ∠BAP = ∠DAP. If AD = 10 cm, then CD =
In a quadrilateral ABCD, ∠A + ∠C is 2 times ∠B + ∠D. If ∠A = 140° and ∠D = 60°, then ∠B=
In the given figure, ∠A = 64°, ∠ABC = 58°. If BO and CO are the bisectors of ∠ABC and ∠ACB respectively of ΔABC, find x° and y°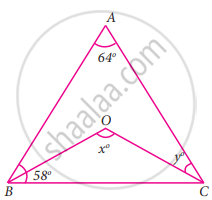
In the given Figure, if AB = 2, BC = 6, AE = 6, BF = 8, CE = 7, and CF = 7, compute the ratio of the area of quadrilateral ABDE to the area of ΔCDF. (Use congruent property of triangles)
