Advertisements
Advertisements
प्रश्न
In below fig. ABCD is a parallelogram and E is the mid-point of side B If DE and AB when produced meet at F, prove that AF = 2AB.
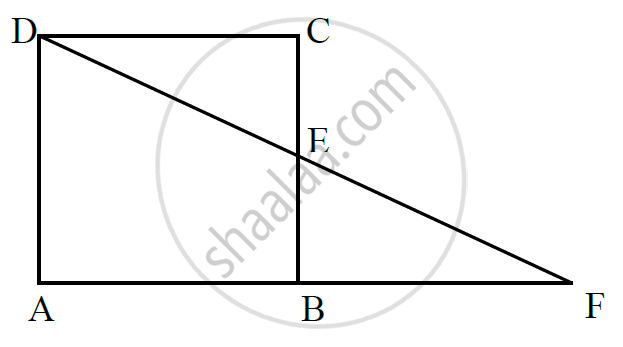
उत्तर
In Δ BEF and ΔCED
`∠`BEF = `∠`CED [Verified opposite angle]
BE = CE [ ∵ E is the mid-point of BC]
`∠`EBF = `∠`ECD [∵ Alternate interior angles are equal]
∴ ∇ BEF ≅ Δ CED [Angle side angle congruence]
∴ BF = CD [Corresponding Parts of Congruent Triangles]
AF = AB + AF
AF = AB + AB
AF = 2 AB
APPEARS IN
संबंधित प्रश्न
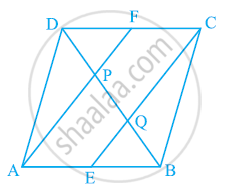
ABCD is a rhombus and P, Q, R and S are the mid-points of the sides AB, BC, CD and DA respectively. Show that the quadrilateral PQRS is a rectangle.
In a parallelogram ABCD, E and F are the mid-points of sides AB and CD respectively (see the given figure). Show that the line segments AF and EC trisect the diagonal BD.
D and F are midpoints of sides AB and AC of a triangle ABC. A line through F and parallel to AB meets BC at point E.
- Prove that BDFE is a parallelogram
- Find AB, if EF = 4.8 cm.
In parallelogram PQRS, L is mid-point of side SR and SN is drawn parallel to LQ which meets RQ produced at N and cuts side PQ at M. Prove that M is the mid-point of PQ.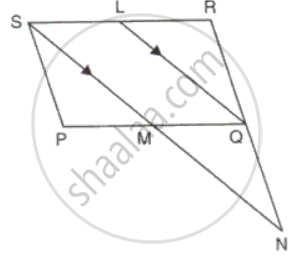
D, E and F are the mid-points of the sides AB, BC and CA of an isosceles ΔABC in which AB = BC. Prove that ΔDEF is also isosceles.
Prove that the straight lines joining the mid-points of the opposite sides of a quadrilateral bisect each other.
In parallelogram ABCD, P is the mid-point of DC. Q is a point on AC such that CQ = `(1)/(4)"AC"`. PQ produced meets BC at R. Prove that
(i) R is the mid-point of BC, and
(ii) PR = `(1)/(2)"DB"`.
In ΔABC, P is the mid-point of BC. A line through P and parallel to CA meets AB at point Q, and a line through Q and parallel to BC meets median AP at point R. Prove that: AP = 2AR
AD is a median of side BC of ABC. E is the midpoint of AD. BE is joined and produced to meet AC at F. Prove that AF: AC = 1 : 3.
In ΔABC, the medians BE and CD are produced to the points P and Q respectively such that BE = EP and CD = DQ. Prove that: A is the mid-point of PQ.
