Advertisements
Advertisements
प्रश्न
ABCD is a rhombus and P, Q, R and S are the mid-points of the sides AB, BC, CD and DA respectively. Show that the quadrilateral PQRS is a rectangle.
उत्तर
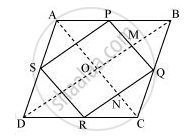
In ΔABC, P and Q are the mid-points of sides AB and BC respectively.
∴ PQ || AC and PQ = `1/2 AC` ...(Using mid-point theorem) ...(1)
In ΔADC,
R and S are the mid-points of CD and AD respectively.
∴ RS || AC and RS = `1/2 AC` ...(Using mid-point theorem) ...(2)
From equations (1) and (2), we obtain
PQ || RS and PQ = RS
Since in quadrilateral PQRS, one pair of opposite sides is equal and parallel to each other, it is a parallelogram.
Let the diagonals of rhombus ABCD intersect each other at point O.
In quadrilateral OMQN,
MQ || ON ...(∵ PQ || AC)
QN || OM ...(∵ QR || BD)
Therefore, OMQN is a parallelogram.
⇒ ∠MQN = ∠NOM
⇒ ∠PQR = ∠NOM
However, ∠NOM = 90° ...(Diagonals of a rhombus are perpendicular to each other)
∴ ∠PQR = 90°
Clearly, PQRS is a parallelogram having one of its interior angles as 90°.
Hence, PQRS is a rectangle.
APPEARS IN
संबंधित प्रश्न
ABCD is a rhombus, EABF is a straight line such that EA = AB = BF. Prove that ED and FC when produced meet at right angles
In triangle ABC, AD is the median and DE, drawn parallel to side BA, meets AC at point E.
Show that BE is also a median.
ABCD is a quadrilateral in which AD = BC. E, F, G and H are the mid-points of AB, BD, CD and Ac respectively. Prove that EFGH is a rhombus.

In ΔABC, AB = 12 cm and AC = 9 cm. If M is the mid-point of AB and a straight line through M parallel to AC cuts BC in N, what is the length of MN?
In ΔABC, BE and CF are medians. P is a point on BE produced such that BE = EP and Q is a point on CF produced such that CF = FQ. Prove that: QAP is a straight line.
ABCD is a kite in which BC = CD, AB = AD. E, F and G are the mid-points of CD, BC and AB respectively. Prove that: ∠EFG = 90°
In ΔABC, D, E and F are the midpoints of AB, BC and AC.
Show that AE and DF bisect each other.
The quadrilateral formed by joining the mid-points of the sides of a quadrilateral PQRS, taken in order, is a rhombus, if ______.
D, E and F are the mid-points of the sides BC, CA and AB, respectively of an equilateral triangle ABC. Show that ∆DEF is also an equilateral triangle.
Prove that the line joining the mid-points of the diagonals of a trapezium is parallel to the parallel sides of the trapezium.
