Advertisements
Advertisements
प्रश्न
The diameter of the circle is 52 cm and the length of one of its chord is 20 cm. Find the distance of the chord from the centre
उत्तर
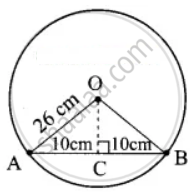
Length of the chord = 20 cm
AC = `20/2`
= 10 cm
In ΔOAC, OC2 = OA2 – AC2
= 262 – 102
= (26 + 10)(26 – 10)
= 36 × 16
OC = `sqrt(30 xx 16)`
= 6 × 4 cm
= 24 cm
Distance of the chord from the centre = 24 cm.
APPEARS IN
संबंधित प्रश्न
In Fig., if AB = AC, prove that BE = EC
Fill in the blank
A continuous piece of a circle is ............... of the circle
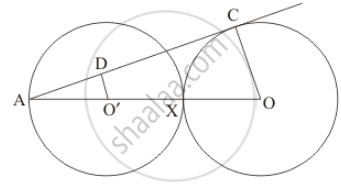
Equal circles with centres O and O' touch each other at X. OO' produced to meet a circle with centre O', at A. AC is a tangent to the circle whose centre is O. O'D is perpendicular to AC. Find the value of\[\frac{DO'}{CO}\]
Find the diameter of the circle if the length of a chord is 3.2 cm and itd distance from the centre is 1.2 cm.
In the given figure, chord EF || chord GH. Prove that, chord EG ≅ chord FH. Fill in the blanks and write the proof.

Use the figure given below to fill in the blank:
If PQ is 8 cm long, the length of RS = ________

Two circles of radii 5 cm and 3 cm intersect at two points and the distance between their centres is 4 cm. Find the length of the common chord
Find the diameter of the circle
Radius = 8 cm
Prove that angle bisector of any angle of a triangle and perpendicular bisector of the opposite side if intersect, they will intersect on the circumcircle of the triangle.
From the figure, identify a sector.

