Advertisements
Advertisements
प्रश्न
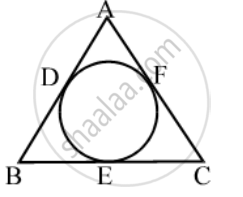
In Fig., if AB = AC, prove that BE = EC
उत्तर
Since tangents from an exterior point to a circle are equal in length.
∴ AD = AF [Tangents from A]
BD = BE [Tangents from B]
CE = CF [Tangents from C]
Now,
AB = AC
⇒ AB – AD = AC – AD [Subtracting AD from both sides]
⇒ AB – AD = AC – AF [Using (i)]
⇒ BD = CF ⇒ BE = CF [Using (ii)]
⇒ BE = CE [Using (iii)]
APPEARS IN
संबंधित प्रश्न
Two circles touch each other externally at P. AB is a common tangent to the circles touching them at A and B. The value of ∠ L APB is
(A) 30°
(B) 45°
(C) 60°
(D) 90°
A point P is 13 cm from the centre of the circle. The length of the tangent drawn from P to the circle is 12cm. Find the radius of the circle.
In two concentric circles, a chord of length 8 cm of the large circle touches the smaller circle. If the radius of the larger circle is 5 cm, then find the radius of the smaller circle.
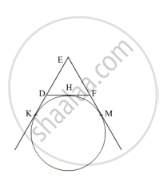
In Fig 2, a circle touches the side DF of ΔEDF at H and touches ED and EF produced at K and M respectively. If EK = 9 cm, then the perimeter of ΔEDF (in cm) is:
In the given figure, if chords AB and CD of the circle intersect each other at right angles, then x + y =
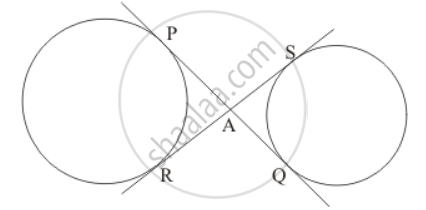
In the given figure, common tangents PQ and RS to two circles intersect at A. Prove that PQ = RS.
In following fig. ABC is an equilateral triangle . A circle is drawn with centre A so that ot cuts AB and AC at M and N respectively. Prove that BN = CM.

In the given circle with diameter AB, find the value of x.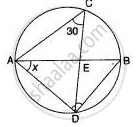
In the following figure, if AOB is a diameter of the circle and AC = BC, then ∠CAB is equal to ______.

If A, B, C and D are four points such that ∠BAC = 45° and ∠BDC = 45°, then A, B, C, D are concyclic.
