Advertisements
Advertisements
प्रश्न
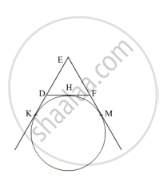
In Fig 2, a circle touches the side DF of ΔEDF at H and touches ED and EF produced at K and M respectively. If EK = 9 cm, then the perimeter of ΔEDF (in cm) is:
विकल्प
A. 18
B. 13.5
C. 12
D. 9
उत्तर
EK = 9 cm
As length of tangents drawn from an external point to the circle are equal.
∴EK = EM = 9 cm
Also, DH = DK and FH = FM … (i)
EK = EM = 9 cm
⇒ ED + DK = 9 cm and EF + FM = 9 cm
⇒ ED + DH = 9 cm and EF + HF = 9 cm [From equation (i)] … (ii)
Perimeter of ΔEDF = ED + DF + EF
= ED + DH + HF + EF
= (9 + 9) cm [From equation (ii)]
= 18 cm
Hence, the correct option is A.
संबंधित प्रश्न
Fill in the blanks:
An arc is a __________ when its ends are the ends of a diameter.
In the adjoining figure, a circle touches all the four sides of a quadrilateral ABCD whose sides are AB=6cm, BC=9cm and CD=8 cm. Find the length of side AD.
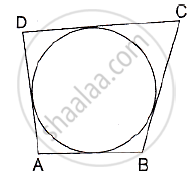
A quadrilateral ABCD is drawn to circumscribe a circle. Prove that AB + CD = AD + BC ?
In the given figure, ABCD is a cyclic quadrilateral. If ∠BCD = 100° and ∠ABD = 70°, find ∠ADB.

If ABCD is a cyclic quadrilateral in which AD || BC (In the given figure). Prove that ∠B = ∠C.

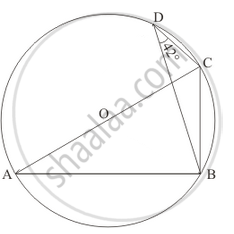
In the given figure, O is the centre of the circle and ∠BDC = 42°. The measure of ∠ACB is
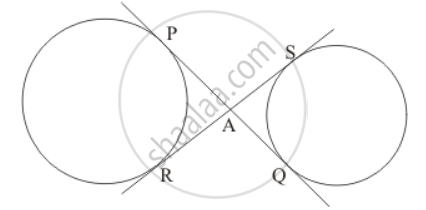
In the given figure, common tangents PQ and RS to two circles intersect at A. Prove that PQ = RS.
In the figure, a circle touches all the sides of quadrilateral ABCD from the inside. The center of the circle is O. If AD⊥ DC and BC = 38, QB = 27, DC = 25, then find the radius of the circle.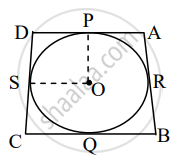
A point A is 26 cm away from the centre of a circle and the length of the tangent drawn from A to the circle is 24 cm. Find the radius of the circle.
If AB = 12 cm, BC = 16 cm and AB is perpendicular to BC, then the radius of the circle passing through the points A, B and C is ______.
