Advertisements
Advertisements
प्रश्न
In the figure, a circle touches all the sides of quadrilateral ABCD from the inside. The center of the circle is O. If AD⊥ DC and BC = 38, QB = 27, DC = 25, then find the radius of the circle.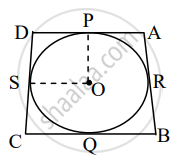
उत्तर
Given: AD ⊥ DC
BC = 38, QB = 27, DC = 25
To find: Radius of the circle, i.e., OP.
Solution:
BC = 38 ......[Given]
∴ BQ + QC = 38 ......[B–Q–C]
∴ 27 + QC = 38 .......[Given]
∴ QC = 38 – 27
∴ QC = 11 units ......(i)
Now, QC = SC ......[Tangent segment theorem]
∴ SC = 11 units .....(ii) [From (i)]
DC = 25 .......[Given]
∴ DS + SC = 25 ......[D–S–C]
∴ DS + 11 = 25 ......[From (ii)]
∴ DS = 25 – 11
∴ DS = 14 units ......(iii)
In ▢DSOP,
∠P = ∠S = 90° ......[Tangent theorem]
∠D = 90° ......[Given]
∴ ∠O = 90° ......[Remaning angle of ▢DSOP]
∴ ▢DSOP is a rectangle.
Also, OP = OS ......[Radii of the same circle]
∴ ▢DSOP is a square .......`[("A rectangle is square if its"),("adjacent sides are congruent")]`
∴ OS = DS = DP = PO .....(iv) [Sides of the square]
∴ OP = 14 units ......[From (iii) and (iv)]
∴ The radius of the circle is 14 units.
APPEARS IN
संबंधित प्रश्न
ABC is a right triangle, right angled at B. A circle is inscribed in it. The lengths of the two sides containing the right angle are 6 cm and 8 cm. Find the radius of the incircle.
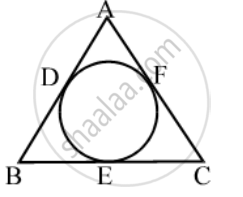
In Fig., if AB = AC, prove that BE = EC
In fig., O is the centre of the circle, PA and PB are tangent segments. Show that the quadrilateral AOBP is cyclic.
Fill in the blanks:
An arc is a __________ when its ends are the ends of a diameter.
If from any point on the common chord of two intersecting circles, tangents be drawn to circles, prove that they are equal.
If the quadrilateral sides touch the circle prove that sum of pair of opposite sides is equal to the sum of other pair.
In fig. a circle touches all the four sides of quadrilateral ABCD with AB = 6cm, BC = 7cm, CD = 4cm. Find AD.
Find the length of tangent drawn to a circle with radius 8 cm form a point 17 cm away from the center of the circle
In the given figure, a triangle ABC is drawn to circumscribe a circle of radius 3 cm such that the segments BC and DC into which BC is divided by the point of contact D, are of
lengths 6cm and 9cm respectively. If the area of 2 ΔABC = 54cm2 then find the lengths of sides AB and AC.

A chord of a circle of radius 14 cm subtends an angle of 120° at the centre. Find the area of the corresponding minor segment of the circle. `[User pi22/7 and sqrt3=1.73]`
In the given figure, O is the centre of the circle and ∠DAB = 50° . Calculate the values of xand y.

If O is the centre of a circle of radius r and AB is a chord of the circle at a distance r/2 from O, then ∠BAO =
In the given figure, chords AD and BC intersect each other at right angles at a point P. If ∠DAB = 35°, then

In the given figure, BDC is a tangent to the given circle at point D such that BD = 30 cm and CD = 7 cm. The other tangents BE and CF are drawn respectively from B and C to the circle and meet when produced at A making BAC a right angle triangle. Calculate (i) AF

AB is a chord of a circle with centre O , AOC is a diameter and AT is the tangent at A as shown in Fig . 10.70. Prove that \[\angle\]BAT = \[\angle\] ACB.
Find the length of the chord of a circle in the following when:
Radius is 6.5 cm and the distance from the centre is 2.5 cm
State, if the following statement is true or false:
The longest chord of a circle is its diameter.
Find the length of the chord AC where AB and CD are the two diameters perpendicular to each other of a circle with radius `4sqrt(2)` cm and also find ∠OAC and ∠OCA
In the given figure, AB is the diameter of the circle. Find the value of ∠ACD.
If angle between two tangents drawn from a point P to a circle of radius a and centre O is 60°, then OP = `asqrt(3)`
