Advertisements
Advertisements
प्रश्न
A chord of a circle of radius 14 cm subtends an angle of 120° at the centre. Find the area of the corresponding minor segment of the circle. `[User pi22/7 and sqrt3=1.73]`
उत्तर
Let O be the centre of the circle and AB be the chord that subtends an angle of 120° at the centre.
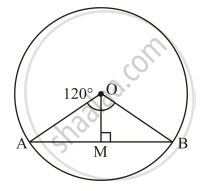
Here, OM ⊥ AB.
Radius of the circle, r = 14 cm
Area of the minor segment = Area of sector OAB − area of ΔAOB
`text{Area of sector OAB}=O/ /360^@ xx pi r^2`
`=120^@/360^@xx22/7xx(14 cm)^2`
`=1/3xx22/7xx196 cm^2`
`=616/3 cm^2`
Now ,OM ⊥ AB.
`∴AM =MB =1/2AB` [Perpendicular from the centre to the bisects the chord]
`rArr AB =2AM `
⇒ AB = 2AM
In ΔOAM and ΔOBM:
OA = OB [Radii of the same circle]
OM = OM [Common]
∠OMA = ∠OMB [Each 90°]
∴ ΔOAM ≅ ΔOBM [RHS congruence criterion]
⇒ ∠AOM = ∠BOM [C.P.C.T]
`∴∠AOM =∠BOM= 120^@/2=60^@`
In ΔAOD:
`rArr sqrt3/2=(AM)/(OA), cos 60^@=(OM)/(OA)`
`rArr sqrt3/2=(AM)/(14 cm),1/2 = (OM)/(14cm)`
`∴ AB=2AM=14sqrt3cm`
`\text{Area} (Δ AOB)=1/2xxABxxOM=1/2xx14sqrt3xx7cm^2=49sqrt3cm^2`
`\text{Area of minor segment}=616/3 cm^2 -49 sqrt3 cm^2`
`=205.33cm^2-49xx1.73cm^2`
`=205.33cm^2-84.77 cm^2`
`=120.56 cm ^2`
Thus, the area of the minor segment is 120.56 cm2.
APPEARS IN
संबंधित प्रश्न
A circle touches the side BC of a ΔABC at a point P and touches AB and AC when produced at Q and R respectively. As shown in the figure that AQ = `1/2` (Perimeter of ΔABC).

The perimeter (in cm) of a square circumscribing a circle of radius a cm, is
In a cyclic quadrilateral ABCD if AB || CD and ∠B = 70°, find the remaining angles.
Can the length of a chord of a circle be greater than its diameter ? Explain.
Find the missing values in the following table for the circles with radius (r), diameter (d) and Circumference (C).
| radius (r) | diameter (d) | Circumference (C) |
| 15 cm |
In the figure, a circle with center P touches the semicircle at points Q and C having center O. If diameter AB = 10, AC = 6, then find the radius x of the smaller circle.
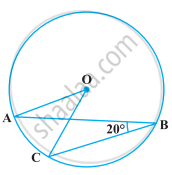
In the following figure, if ∠ABC = 20º, then ∠AOC is equal to ______.
In the following figure, BC is a diameter of the circle and ∠BAO = 60º. Then ∠ADC is equal to ______.
What is the area of a semi-circle of diameter ‘d’?
Find the length of the arc of a circle which subtends an angle of 60° at the centre of the circle of radius 42 cm.
