Advertisements
Advertisements
प्रश्न
In the following figure, BC is a diameter of the circle and ∠BAO = 60º. Then ∠ADC is equal to ______.
विकल्प
30º
45º
60º
120º
उत्तर
In the following figure, BC is a diameter of the circle and ∠BAO = 60º. Then ∠ADC is equal to 60º.
Explanation:
Given: BC is a diameter of the circle and ∠BAO = 60º.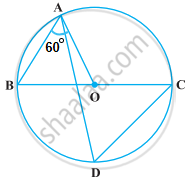
Now, in triangle OAB,
OA = OB ...[Radii of the same circle]
So, ∠ABO = ∠BAO ...[Angle opposite to equal sides are equal]
∠ABO = ∠BAO = 60º ...[Given]
Now, ∠ADC = ∠ABC = 60º ...[∠ADC and ∠ABC are angles in the same segment of a circle are equal]
Therefore, ∠ADC = 60º.
APPEARS IN
संबंधित प्रश्न
In fig., O is the centre of the circle, PA and PB are tangent segments. Show that the quadrilateral AOBP is cyclic.
Fill in the blank
A continuous piece of a circle is ............... of the circle
From an external point P, tangents PA and PB are drawn to a circle with center O. If CD is the tangent to the circle at a point E and PA = 14cm, find the perimeter of ΔPCD.

In a cyclic quadrilateral ABCD, if m ∠A = 3 (m ∠C). Find m ∠A.
In the given figure, OQ : PQ = 3.4 and perimeter of Δ POQ = 60 cm. Determine PQ, QR and OP.
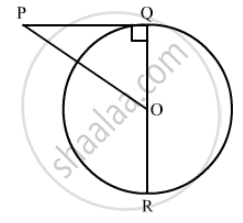
In the given figure, PO \[\perp\] QO. The tangents to the circle at P and Q intersect at a point T. Prove that PQ and OTare right bisector of each other.

If the radius of a circle is 5 cm, what will its diameter be?
The diameter of the circle is 52 cm and the length of one of its chord is 20 cm. Find the distance of the chord from the centre
In the figure, O is the centre of the circle, and ∠AOB = 90°, ∠ABC = 30°. Then find ∠CAB.

In a right triangle ABC in which ∠B = 90°, a circle is drawn with AB as diameter intersecting the hypotenuse AC and P. Prove that the tangent to the circle at P bisects BC.
