Advertisements
Advertisements
प्रश्न
In the figure, a circle with center P touches the semicircle at points Q and C having center O. If diameter AB = 10, AC = 6, then find the radius x of the smaller circle.
उत्तर
Given: AB = 10 units, AC = 6 units, PC = PQ = x unit.
To find: x
Solution:
Diameter AB = 10 ...[Given]
∴ Radius = `1/2 xx "AB" = 1/2 xx 10` = 5.
∴ OQ = AO = OB = 5 ......(i)
AC = AO + OC .....[A–O–C]
∴ OC = AC – AO
∴ OC = 6 – 5 ......[Given and (i)]
∴ OC = 1 ......(ii)
OQ = OP + PQ ......[O–P–Q]
∴ OP = OQ – PQ
= 5 – x ......(iii) [From (i) and given]
Note that seg AB is tangent to the given smaller circle at point C.
∴ ∠PCO = 90° ......[Tangent theorem]
∴ In ∆PCO,
∠PCO = 90°
∴ OP2 = PC2 + OC2 ......[Pythagoras theorem]
∴ (5 – x)2 = x2 + (1)2 ......[From (ii) and (iii)]
∴ 25 – 10x + x2 = x2 + 1
∴ 10x = 24
∴ x = `24/10` = 2.4
∴ The radius x of the smaller circle is 2.4 units
APPEARS IN
संबंधित प्रश्न
Suppose You Are Given a Circle. Give a Construction to Find Its Centre.
Find the length of tangent drawn to a circle with radius 8 cm form a point 17 cm away from the center of the circle
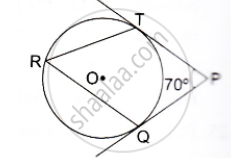
In the given figure, O is the centre of a circle. PT and PQ are tangents to the circle from an external point P. If ∠TPQ = 70° , find the ∠TRQ.
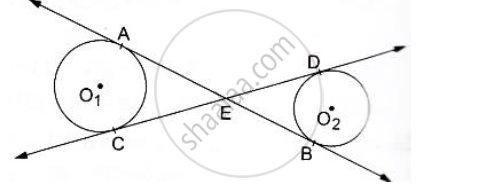
In the given figure common tangents AB and CD to the two circles with centres O1 and O2 intersect at E. Prove that AB=CD
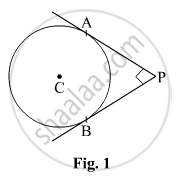
In Fig. 1, PA and PB are two tangents drawn from an external point P to a circle with centre C and radius 4 cm. If PA ⊥ PB, then the length of each tangent is:
In the given figure, O is the centre of the circle. Find ∠CBD.

A chord of length 14 cm is at a distance of 6 cm from the centre of a circle. The length of another chord at a distance of 2 cm from the centre of the circle is
One chord of a circle is known to be 10 cm. The radius of this circle must be
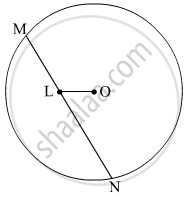
In the given figure, seg MN is a chord of a circle with centre O. MN = 25, L is a point on chord MN such that ML = 9 and d(O,L) = 5. Find the radius of the circle.
ABC is a right triangle in which ∠B = 90°. If AB = 8 cm and BC = 6 cm, find the diameter of the circle inscribed in the triangle.
Use the figure given below to fill in the blank:
EF is a ______ of the circle.

In the adjoining figure, seg DE is the chord of the circle with center C. seg CF⊥ seg DE and DE = 16 cm, then find the length of DF?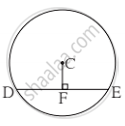
From a point P which is at a distance of 13 cm from the centre O of a circle of radius 5 cm, the pair of tangents PQ and PR to the circle are drawn. Then the area of the quadrilateral PQOR is ______
In the given figure, point P is 26 cm away from the centre O of a circle and the length PT of the tangent drawn from P to the circle is 24 cm. Then the radius of the circle is ______
C(O, r1) and C(O, r2) are two concentric circles with r1 > r2 AB is a chord of C(O, r1) touching C(O, r2) at C then ______
A point P is 10 cm from the center of a circle. The length of the tangent drawn from P to the circle is 8 cm. The radius of the circle is equal to ______
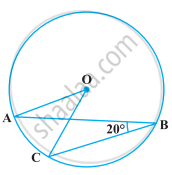
In the following figure, if ∠ABC = 20º, then ∠AOC is equal to ______.
A quadrilateral ABCD is inscribed in a circle such that AB is a diameter and ∠ADC = 130º. Find ∠BAC.
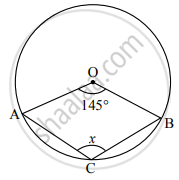
In the given figure, O is the centre of the circle. If ∠ AOB = 145°, then find the value of x.