Advertisements
Advertisements
प्रश्न
In the given figure common tangents AB and CD to the two circles with centres O1 and O2 intersect at E. Prove that AB=CD
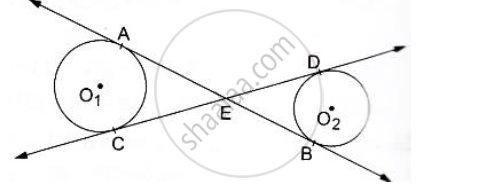
उत्तर
We know that tangent segments to a circle from the same external point are congruent.
So, we have
EA = EC for the circle having center O1
and
ED = EB for the circle having center O1
Now, Adding ED on both sides in EA = EC. we get
EA+ ED = EC + ED
⇒ EA + EB = EC + ED
⇒ AB = CD
APPEARS IN
संबंधित प्रश्न
Prove that the line segment joining the point of contact of two parallel tangents to a circle is a diameter of the circle.
A chord PQ of a circle of radius 10 cm substends an angle of 60° at the centre of circle. Find the area of major and minor segments of the circle.
If PA and PB are tangents from an outside point P. such that PA = 10 cm and ∠APB = 60°. Find the length of chord AB.
Suppose You Are Given a Circle. Give a Construction to Find Its Centre.
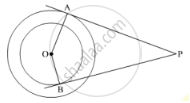
Tangents PA and PB are drawn from an external point P to two concentric circles with centre O and radii 8 cm and 5 cm respectively, as shown in Fig. 3. If AP = 15 cm, then find the length of BP.
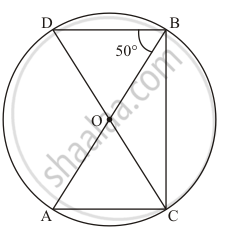
In the given figure, AB and CD are diameters of a circle with centre O. If ∠OBD = 50°, find ∠AOC.
Draw a circle of diameter 7 cm. Draw two radii of this circle such that the angle between these radii is 90°. Shade the minor sector obtained. Write a special name for this sector.
Find the length of the chord AC where AB and CD are the two diameters perpendicular to each other of a circle with radius `4sqrt(2)` cm and also find ∠OAC and ∠OCA
Twice the radius is ________________
Circles with centres A, B and C touch each other externally. If AB = 36, BC = 32, CA = 30, then find the radii of each circle.
