Advertisements
Advertisements
प्रश्न
Circles with centres A, B and C touch each other externally. If AB = 36, BC = 32, CA = 30, then find the radii of each circle.
उत्तर
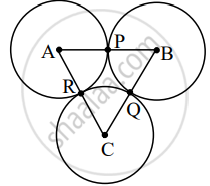
Given: AB = 36, BC = 32, CA = 30
To Find: Radii of each circle.
Solution:
Let x, y, z be the radii of the circles with centers A, B, C respectively.
∴ AP = RA = x, PB = BQ = y, CR = QC = z
AB = AP + PB ....[A–P–B]
∴ 36 = x + y ...(ii) [From (i) and given]
BC = BQ + QC ....[B – Q – C]
∴ 32 = y + z .....(iii) [From (i) and given]
CA = CR + RA ......[C – R – A]
∴ 30 = z + x ......(iv) [From (i) and given]
Now,
AB + BC + CA = 36 + 32 + 30
∴ (AP + PB) + (BQ + QC) + (CR + RA) = 98 ......[A–P–B, B–Q–C, C–R–A]
∴ (x + y) + (y + z) + (z + x) = 98 ......[From (i)]
∴ 2x + 2y + 2z = 98
∴ 2(x + y + z) = 98
∴ x + y + z = `98/2`
∴ x + y + z = 49
∴ (x + y) + z = 49 .....[From (ii)]
∴ 36 + z = 49
∴ z = 49 – 36
∴ z = 13 ......(v)
y + z = 32 ......[From (iii)]
∴ y + 13 = 32 ......[From (v)]
∴ y = 32 – 13
∴ y = 19
z + x = 30 .....[From (iv)]
∴ 13 + x = 30 .....[From (v)]
∴ x = 30 – 13
∴ x = 17
APPEARS IN
संबंधित प्रश्न
If AB, AC, PQ are tangents in Fig. and AB = 5cm find the perimeter of ΔAPQ.
If ΔABC is isosceles with AB = AC and C (0, 2) is the in circle of the ΔABC touching BC at L, prove that L, bisects BC.
In fig. there are two concentric circles with Centre O of radii 5cm and 3cm. From an
external point P, tangents PA and PB are drawn to these circles if AP = 12cm, find the
tangent length of BP.
In the below fig. O is the centre of the circle. If ∠APB = 50°, find ∠AOB and ∠OAB.

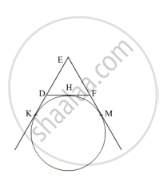
In Fig 2, a circle touches the side DF of ΔEDF at H and touches ED and EF produced at K and M respectively. If EK = 9 cm, then the perimeter of ΔEDF (in cm) is:
In following figure, three circles each of radius 3.5 cm are drawn in such a way that each of them touches the other two. Find the area enclosed between these three circles (shaded region). `["Use" pi=22/7]`

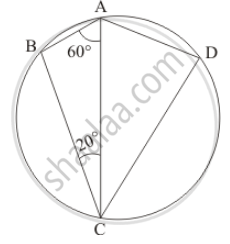
In the given figure, if ∠BAC = 60° and ∠BCA = 20°, find ∠ADC.
In the given figure, O is the centre of the circle and BCD is tangent to it at C. Prove that ∠BAC + ∠ACD = 90°.

In the given figure, the area enclosed between the two concentric circles is 770 cm2. If the radius of the outer circle is 21 cm, calculate the radius of the inner circle.
Use the figure given below to fill in the blank:
Diameter of a circle is ______.

Construct a triangle PQR with QR = 5.5 cm, ∠Q = 60° and angle R = 45°. Construct the circumcircle cif the triangle PQR.
A chord is 12 cm away from the centre of the circle of radius 15 cm. Find the length of the chord
In a circle, AB and CD are two parallel chords with centre O and radius 10 cm such that AB = 16 cm and CD = 12 cm determine the distance between the two chords?
A line segment which joins any two points on a circle is a ___________
Given: A circle inscribed in a right angled ΔABC. If ∠ACB = 90° and the radius of the circle is r.
To prove: 2r = a + b – c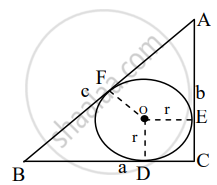
If the angle between two tangents drawn from a point P to a circle of radius ‘a’ and centre ‘O’ is 90°, then OP = ______
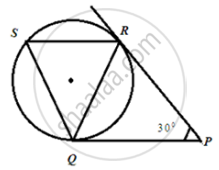
In the following figure, tangents PQ and PR are drawn to a circle such that ∠RPQ = 30°. A chord RS is drawn parallel to the tangent PQ, then ∠RQS.
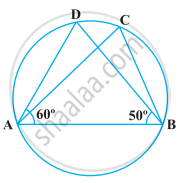
In the following figure, if ∠DAB = 60º, ∠ABD = 50º, then ∠ACB is equal to ______.
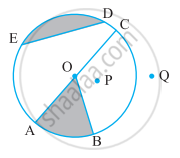
From the figure, identify a diameter.
Assertion (A): If the circumference of a circle is 176 cm, then its radius is 28 cm.
Reason (R): Circumference = 2π × radius of a circle.
