Advertisements
Advertisements
प्रश्न
In the given figure, O is the centre of the circle and BCD is tangent to it at C. Prove that ∠BAC + ∠ACD = 90°.

उत्तर
In the given figure, let us join D an A.

Consider `ΔOCA`. We have,
OC = OA (Radii of the same circle)
We know that angles opposite to equal sides of a triangle will be equal. Therefore,
`∠OCA =∠OAC ` … (1)
It is clear from the figure that
`∠DCA +∠OCA=∠OCD`
Now from (1)
`∠DCA +∠OAC =∠OCD`
Now as BD is tangent therefore, `∠OCD=90^circ.`
Therefore `∠DCA +∠OAC = 90^circ`
From the figure we can see that `∠OAC =∠BAC`
`∠DAC + ∠BAC = 90^o`
Thus, we have proved.
संबंधित प्रश्न
Prove that in two concentric circles, the chord of the larger circle which touches the smaller circle, is bisected at the point of contact.
In figure 1, O is the centre of a circle, PQ is a chord and PT is the tangent at P.
If ∠POQ = 70°, then ∠TPQ is equal to

Number of circles that can be drawn through three non-collinear points is
In the given figure, if ∠ABC = 45°, then ∠AOC =
In the given figure, PO \[\perp\] QO. The tangents to the circle at P and Q intersect at a point T. Prove that PQ and OTare right bisector of each other.

Find the length of the chord of a circle in the following when:
Radius is 6.5 cm and the distance from the centre is 2.5 cm
If the radius of a circle is 5 cm, what will its diameter be?
A, B, C are any points on the circle with centre O. If m(arc BC) = 110° and m(arc AB) = 125°, find measure arc AC.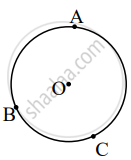
If the angle between two radii of a circle is 130°, then the angle between the tangents at the ends of the radii is ______
A point P is 10 cm from the center of a circle. The length of the tangent drawn from P to the circle is 8 cm. The radius of the circle is equal to ______
