Advertisements
Advertisements
प्रश्न
A, B, C are any points on the circle with centre O. If m(arc BC) = 110° and m(arc AB) = 125°, find measure arc AC.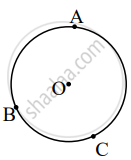
उत्तर
m(arc AB) + m(arc BC) + m(arc AC) = 360° ......[Measure of complete circle is 360°]
∴ 125° + 110° + m(arc AC) = 360°
∴ m(arc AC) = 360° – 125° – 110°
= 125°
APPEARS IN
संबंधित प्रश्न
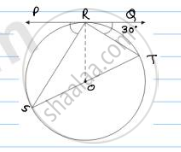
In Fig below, PQ is tangent at point R of the circle with center O. If ∠TRQ = 30°. Find
∠PRS.
Fill in the blank
Circles having the same centre and different radii are called ...........................circles.
Find the length of tangent drawn to a circle with radius 8 cm form a point 17 cm away from the center of the circle
In the given figure, a triangle ABC is drawn to circumscribe a circle of radius 3 cm such that the segments BC and DC into which BC is divided by the point of contact D, are of
lengths 6cm and 9cm respectively. If the area of 2 ΔABC = 54cm2 then find the lengths of sides AB and AC.

In fig. 3 are two concentric circles of radii 6 cm and 4 cm with centre O. If AP is a tangent to the larger circle and BP to the smaller circle and length of AP is 8 cm, find the length of BP ?

In the given figure, ABC is a right triangle right-angled at B such that BC = 6 cm and AB = 8 cm. Find the radius of its incircle.

Choose correct alternative answer and fill in the blank.
Radius of a circle is 10 cm and distance of a chord from the centre is 6 cm. Hence the length of the chord is .........
Length of a chord of a circle is 24 cm. If distance of the chord from the centre is 5 cm, then the radius of that circle is ______.

In the above figure, `square`XLMT is a rectangle. LM = 21 cm, XL = 10.5 cm. Diameter of the smaller semicircle is half the diameter of the larger semicircle. Find the area of non-shaded region.

In the above figure, seg AB is a diameter of a circle with centre P. C is any point on the circle. seg CE ⊥ seg AB. Prove that CE is the geometric mean of AE and EB. Write the proof with the help of the following steps:
a. Draw ray CE. It intersects the circle at D.
b. Show that CE = ED.
c. Write the result using the theorem of the intersection of chords inside a circle. d. Using CE = ED, complete the proof.
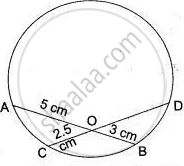
In Fig., chords AB and CD of the circle intersect at O. AO = 5 cm, BO = 3 cm and CO = 2.5 cm. Determine the length of DO.
Draw circle with diameter: 6 cm
In above case, measure the length of the radius of the circle drawn.
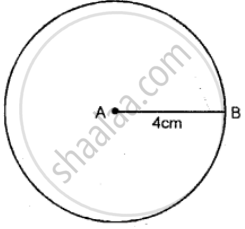
Mark two points A and B ,4cm a part, Draw a circle passing through B and with A as a center
Two circles of radii 5 cm and 3 cm intersect at two points and the distance between their centres is 4 cm. Find the length of the common chord
A point A is 26 cm away from the centre of a circle and the length of the tangent drawn from A to the circle is 24 cm. Find the radius of the circle.
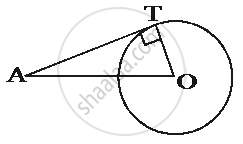
The length of the tangent from point A to a circle, of radius 3 cm, is 4 cm. The distance of A from the centre of the circle is ______
If A, B, C, D are four points such that ∠BAC = 30° and ∠BDC = 60°, then D is the centre of the circle through A, B and C.
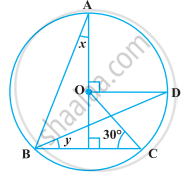
In the following figure, O is the centre of the circle, ∠BCO = 30°. Find x and y.
If radius of a circle is 5 cm, then find the length of longest chord of a circle.
Assertion (A): If the circumference of a circle is 176 cm, then its radius is 28 cm.
Reason (R): Circumference = 2π × radius of a circle.
