Advertisements
Advertisements
प्रश्न
In the following figure, O is the centre of the circle, ∠BCO = 30°. Find x and y.
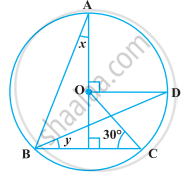
उत्तर
Given, O is the centre of the circle and ∠BCO = 30°. In the given figure join OB and AC.
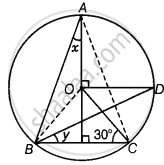
In ΔBOC, CO = BO ...[Both are the radius of circle]
∴ ∠OBC = ∠OCB = 30° ...[Angles opposite to equal sides are equal]
∴ ∠BOC = 180° – (∠OBC + ∠OCE) ...[By angle sum property of a triangle]
= 180° – (30° + 30°)
= 120°
∠BOC = 2∠BAC
We know that, in a circle, the angle subtended by an arc at the centre is twice the angle subtended by it at the remaining part of the circle.
∴ `∠BAC = 120^circ/2 = 60^circ`
Also, ∠BAE = ∠CAE = 30° ...[AE is an angle bisector of angle A]
⇒ ∠BAE = x = 30°
In ΔABE, ∠BAE + ∠EBA + ∠AEB = 180° ...[By angle sum property of a triangle]
⇒ 30° + ∠EBA + 90° = 180°
∴ ∠EBA = 180° – (90° + 30°)
= 180° – 120°
= 60°
Now, ∠EBA = 60°
⇒ ∠ABD + y = 60°
⇒ `1/2 xx ∠AOD + y = 60^circ` ...[In a circle, the angle subtended by an arc at the centre is twice the angle subtended by it at the remaining part of the circle]
⇒ `90^circ/2 + y = 60^circ` ...[∵ ∠AOD = 90°, given]
⇒ 45° + y = 60°
⇒ y = 60° – 45°
∴ y = 15°
APPEARS IN
संबंधित प्रश्न
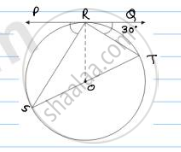
In Fig below, PQ is tangent at point R of the circle with center O. If ∠TRQ = 30°. Find
∠PRS.
If ΔABC is isosceles with AB = AC and C (0, 2) is the in circle of the ΔABC touching BC at L, prove that L, bisects BC.
Fill in the blank:
An arc is a ................ when its ends are the ends of a diameter.
Use the figure given below to fill in the blank:
________ is a radius of the circle.
State, if the following statement is true or false:
The diameters of a circle always pass through the same point in the circle.
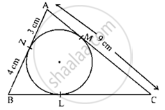
In the adjoining figure, Δ ABC is circumscribing a circle. Then, the length of BC is ______
The circumcentre of the triangle ABC is O. Prove that ∠OBC + ∠BAC = 90º.
A quadrilateral ABCD is inscribed in a circle such that AB is a diameter and ∠ADC = 130º. Find ∠BAC.
In the given figure, O is the centre of the circle. Shade sectors OAC and OPB.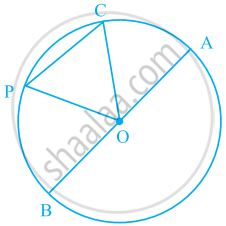
Assertion (A): If the circumference of a circle is 176 cm, then its radius is 28 cm.
Reason (R): Circumference = 2π × radius of a circle.
