Advertisements
Advertisements
प्रश्न
AB and AC are two chords of a circle of radius r such that AB = 2AC. If p and q are the distances of AB and AC from the centre, prove that 4q2 = p2 + 3r2.
उत्तर
Given: In a circle of radius r, there are two chords AB and AC such that AB = 2AC. Also, the distance of AB and AC from the centre are p and q, respectively.
To prove: 4q2 = p2 + 3r2
Proof: Let AC = a, then AB = 2a
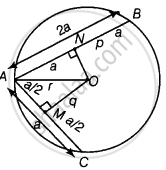
From centre O, perpendicular is drawn to the chords AC and AB at M and N, respectively.
∴ `AM = MC = a/2`
AN = NB = a
In ΔOAM, AO2 = AM2 + MO2 ...[By Pythagoras theorem]
⇒ `AO^2 = (a/2)^2 + q^2` ...(i)
In ΔOAN, use Pythagoras theorem,
AO2 = (AN)2 + (NO)2
⇒ AO2 = (a)2 + p2 ...(ii)
From equations (i) and (ii),
`(a/2)^2 + q^2 = a^2 + p^2`
⇒ `a^2/4 + q^2 = a^2 + p^2`
⇒ a2 + 4q2 = 4a2 + 4p2 ...[Multiplying both sides by 4]
⇒ 4q2 = 3a2 + 4p2
⇒ 4q2 = p2 + 3(a2 + p2)
⇒ 4q2 = p2 + 3r2 ...[In right angled ΔOAN, r2 = a2 + p2]
Hence proved.
APPEARS IN
संबंधित प्रश्न
If two equal chords of a circle intersect within the circle, prove that the segments of one chord are equal to corresponding segments of the other chord.
If a line intersects two concentric circles (circles with the same centre) with centre O at A, B, C, and D, prove that AB = CD (see given figure).

true or false
If a circle is divided into three equal arcs each is a major arc.
An equilateral triangle of side 9cm is inscribed in a circle. Find the radius of the circle.
Two chords AB and CD of lengths 5 cm and 11 cm respectively of a circle are parallel to each other and are opposite side of its center. If the distance between AB and CD is 6 cm. Find the radius of the circle.
Two equal circles of radius r intersect such that each passes through the centre of the other. The length of the common chord of the circle is
If AB is a chord of a circle, P and Q are the two points on the circle different from A and B, then
In a circle of radius 17 cm, two parallel chords are drawn on opposite side of a diameter. The distance between the chords is 23 cm. If the length of one chord is 16 cm, then the length of the other is
Two chords AB and CD of a circle are each at distances 4 cm from the centre. Then AB = CD.
Two congruent circles with centres O and O′ intersect at two points A and B. Then ∠AOB = ∠AO′B.
