Advertisements
Advertisements
प्रश्न
In a circle of radius 17 cm, two parallel chords are drawn on opposite side of a diameter. The distance between the chords is 23 cm. If the length of one chord is 16 cm, then the length of the other is
विकल्प
34 cm
15 cm
23 cm
30 cm
उत्तर
30 cm
Given that: Radius of the circle is 17 cm, distance between two parallel chords AB and CD is 23 cm, where AB= 16 cm. We have to find the length of CD.
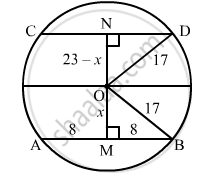
We know that the perpendicular drawn from the centre of the circle to any chord divides it into two equal parts.
So, AM = MB = 8 cm
Let OM = x cm
In triangle OMB,
`x = sqrt(17^2 - 8^2 = 15)`
Now, in triangle OND, ON = (23 − x) cm = (23 − 15) cm = 8 cm
`ND = sqrt(OD^2 -ON^2)`
`⇒ ND = sqrt(17^2 - 8^2 = 15)`
Therefore, the length of the other chord is
`CD = 2 xx 15 = 30 cm `
APPEARS IN
संबंधित प्रश्न
Two circles of radii 5 cm and 3 cm intersect at two points and the distance between their centres is 4 cm. Find the length of the common chord.
If two equal chords of a circle intersect within the circle, prove that the segments of one chord are equal to corresponding segments of the other chord.
An equilateral triangle of side 9cm is inscribed in a circle. Find the radius of the circle.
In a circle with centre O, AB and CD are two diameters perpendicular to each other. The length of chord AC is
Two equal circles of radius r intersect such that each passes through the centre of the other. The length of the common chord of the circle is
Two chords AB and CD of a circle are each at distances 4 cm from the centre. Then AB = CD.
Two congruent circles with centres O and O′ intersect at two points A and B. Then ∠AOB = ∠AO′B.
If two equal chords of a circle intersect, prove that the parts of one chord are separately equal to the parts of the other chord.
Two equal chords AB and CD of a circle when produced intersect at a point P. Prove that PB = PD.
AB and AC are two chords of a circle of radius r such that AB = 2AC. If p and q are the distances of AB and AC from the centre, prove that 4q2 = p2 + 3r2.
