Advertisements
Advertisements
प्रश्न
If two equal chords of a circle intersect within the circle, prove that the segments of one chord are equal to corresponding segments of the other chord.
उत्तर
Let PQ and RS be two equal chords of a given circle and they are intersecting each other at point T.
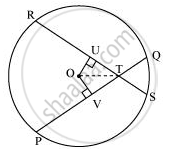
Draw perpendiculars OV and OU on these chords.
In ΔOVT and ΔOUT,
OV = OU ...(Equal chords of a circle are equidistant from the centre)
∠OVT = ∠OUT ...(Each 90°)
OT = OT ...(Common)
∴ ΔOVT ≅ ΔOUT ...(RHS congruence rule)
∴ VT = UT ...(By CPCT) ...(1)
It is given that,
PQ = RS ...(2)
⇒ `1/2PQ` = `1/2RS`
⇒ PV = RU ...(3)
On adding equations (1) and (3), we obtain
PV + VT = RU + UT
⇒ PT = RT ...(4)
By subtracting equation (4) from equation (2), we obtain
PQ − PT = RS − RT
⇒ QT = ST ...(5)
Equations (4) and (5) indicate that the corresponding segments of chords PQ and RS are congruent to each other.
APPEARS IN
संबंधित प्रश्न
Two circles of radii 5 cm and 3 cm intersect at two points and the distance between their centres is 4 cm. Find the length of the common chord.
If a line intersects two concentric circles (circles with the same centre) with centre O at A, B, C, and D, prove that AB = CD (see given figure).

Three girls Reshma, Salma and Mandip are playing a game by standing on a circle of radius 5m drawn in a park. Reshma throws a ball to Salma, Salma to Mandip, Mandip to Reshma. If the distance between Reshma and Salma and between Salma and Mandip is 6m each, what is the distance between Reshma and Mandip?
A circular park of radius 20m is situated in a colony. Three boys Ankur, Syed and David are sitting at equal distance on its boundary each having a toy telephone in his hands to talk each other. Find the length of the string of each phone.
true or false
A circle has only finite number of equal chords.
Angle formed in minor segment of a circle is
In a circle with centre O, AB and CD are two diameters perpendicular to each other. The length of chord AC is
Two equal circles of radius r intersect such that each passes through the centre of the other. The length of the common chord of the circle is
Two congruent circles with centres O and O′ intersect at two points A and B. Then ∠AOB = ∠AO′B.
Two equal chords AB and CD of a circle when produced intersect at a point P. Prove that PB = PD.
