Advertisements
Advertisements
प्रश्न
A circular park of radius 20m is situated in a colony. Three boys Ankur, Syed and David are sitting at equal distance on its boundary each having a toy telephone in his hands to talk each other. Find the length of the string of each phone.
उत्तर
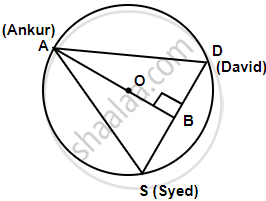
It is given that AS = SD = DA
Therefore, ΔASD is an equilateral triangle.
OA (radius) = 20m
Medians of equilateral triangle pass through the circum centre (O) of the equilateral triangle ASD. We also know that medians intersect each other in the ratio 2 : 1. As AB is the median of equilateral triangle ASD, we can write
`rArr(OA)/(OB)` = `2/1`
`rArr(20m)/(OB)` = `2/1`
`rArrOB =(20/2)m` = 10m
∴ AB = OA + OB = (20 + 10) m = 30m
In ΔABD,
AD2 = AB2 + BD2
AD2 = `(30)^2 + ((AD)/2)^2`
AD2 = `900 + 1/4AD^2`
`3/4AD^2` = 900
AD2 = 1200
AD = `20sqrt3`
Therefore, the length of the string of each phone will be `20sqrt3` m.
APPEARS IN
संबंधित प्रश्न
If two equal chords of a circle intersect within the circle, prove that the segments of one chord are equal to corresponding segments of the other chord.
If a line intersects two concentric circles (circles with the same centre) with centre O at A, B, C, and D, prove that AB = CD (see given figure).

Three girls Reshma, Salma and Mandip are playing a game by standing on a circle of radius 5m drawn in a park. Reshma throws a ball to Salma, Salma to Mandip, Mandip to Reshma. If the distance between Reshma and Salma and between Salma and Mandip is 6m each, what is the distance between Reshma and Mandip?
true or false
If a circle is divided into three equal arcs each is a major arc.
true or false
A circle has only finite number of equal chords.
Two chords AB and CD of lengths 5 cm and 11 cm respectively of a circle are parallel to each other and are opposite side of its center. If the distance between AB and CD is 6 cm. Find the radius of the circle.
Two chords AB and CD of a circle are each at distances 4 cm from the centre. Then AB = CD.
If two equal chords of a circle intersect, prove that the parts of one chord are separately equal to the parts of the other chord.
Two equal chords AB and CD of a circle when produced intersect at a point P. Prove that PB = PD.
AB and AC are two chords of a circle of radius r such that AB = 2AC. If p and q are the distances of AB and AC from the centre, prove that 4q2 = p2 + 3r2.
