Question

Two equal chords AB and CD of a circle when produced intersect at a point P. Prove that PB = PD.

Answer 1

Given: Two equal chords AB and CD of a circle intersecting at a point P.

To prove: PB = PD

Construction: Join OP, draw OL ⊥ AB and OM ⊥ CD

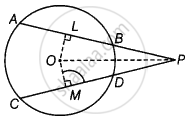
Proof: We have, AB = CD

⇒ OL = OM  ...[Equal chords are equidistant from the centre]

In ΔOLP and ΔOMP,

OL = OM   ...[Proved above]

∠OLP = ∠OMP   ...[Each 90°]

And OP = OP   ...[Common side]

 ∴ ΔOLP ≅ ΔOMP   ...[By RHS congruence rule]

⇒ LP = MP  [By CPCT] ...(i)

Now, AB = CD

⇒ `1/2 (AB) = 1/2 (CD)`  ...[Dividing both sides by 2]

⇒ BL = DM   ...(ii) [Perpendicular drawn from centre to the circle bisects the chord i.e., AL = LB and CM = MD]

On subtracting equation (ii) and equation (i), we get

LP – BL = MP – DM

⇒ PB = PD 

Hence proved.