Advertisements
Advertisements
Question
A, B, C are any points on the circle with centre O. If m(arc BC) = 110° and m(arc AB) = 125°, find measure arc AC.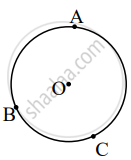
Solution
m(arc AB) + m(arc BC) + m(arc AC) = 360° ......[Measure of complete circle is 360°]
∴ 125° + 110° + m(arc AC) = 360°
∴ m(arc AC) = 360° – 125° – 110°
= 125°
APPEARS IN
RELATED QUESTIONS
Prove that in two concentric circles, the chord of the larger circle which touches the smaller circle, is bisected at the point of contact.
Write True or False. Give reasons for your answers.
A chord of a circle, which is twice as long as its radius, is a diameter of the circle.
A chord PQ of a circle of radius 10 cm substends an angle of 60° at the centre of circle. Find the area of major and minor segments of the circle.
In fig.. O is the center of the circle and BCD is tangent to it at C. Prove that ∠BAC +
∠ACD = 90°
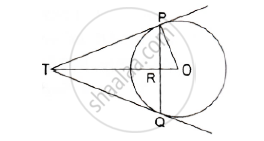
In the given figure, PO⊥QO. The tangents to the circle at P and Q intersect at a point T. Prove that PQ and OT are right bisector of each other.
PQ is a chord of length 4.8 cm of a circle of radius 3cm. The tangents at P and Q intersect at a point T as shown in the figure. Find the length of TP.
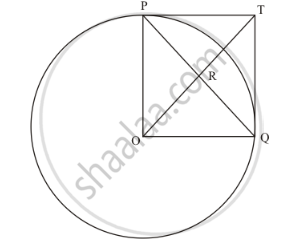
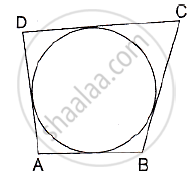
In the adjoining figure, a circle touches all the four sides of a quadrilateral ABCD whose sides are AB=6cm, BC=9cm and CD=8 cm. Find the length of side AD.
Two circles touch internally. The sum of their areas is 116 π cm2 and the distance between their centres is 6 cm. Find the radii of the circles ?
In a cyclic quadrilateral ABCD if AB || CD and ∠B = 70°, find the remaining angles.
If O is the centre of a circle of radius r and AB is a chord of the circle at a distance r/2 from O, then ∠BAO =
Two concentric circles are of diameters 30 cm and 18 cm. Find the length of the chord of the larger circle which touches the smaller circle.
Find the area of a circle of radius 7 cm.
In the given figure, the area enclosed between the two concentric circles is 770 cm2. If the radius of the outer circle is 21 cm, calculate the radius of the inner circle.
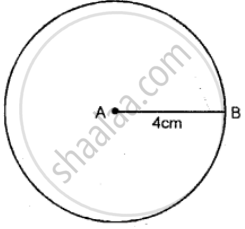
Mark two points A and B ,4cm a part, Draw a circle passing through B and with A as a center
Draw circle with the radii given below.
2 cm
A point P is 10 cm from the center of a circle. The length of the tangent drawn from P to the circle is 8 cm. The radius of the circle is equal to ______
AB is a diameter of a circle and AC is its chord such that ∠BAC = 30°. If the tangent at C intersects AB extended at D, then BC = BD.
In the following figure, if AOB is a diameter of the circle and AC = BC, then ∠CAB is equal to ______.

In the following figure, if AOB is a diameter and ∠ADC = 120°, then ∠CAB = 30°.
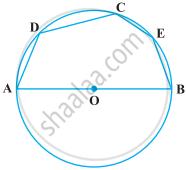
AB is a chord of a circle with centre O. AOC is diameter of circle, AT is a tangent at A.
Write answers of the following questions:
- Draw the figure using the given information.
- Find the measures of ∠CAT and ∠ABC with reasons.
- Whether ∠CAT and ∠ABC are congruent? Justify your answer.
