Advertisements
Advertisements
Question
AB is a diameter of a circle and AC is its chord such that ∠BAC = 30°. If the tangent at C intersects AB extended at D, then BC = BD.
Options
True
False
Solution
This statement is True.
Explanation:
Given: AB is a diameter of circle with center O and AC is a chord such that ∠BAC = 30°
Also tangent at C intersects AB extends at D.
To prove: BC = BD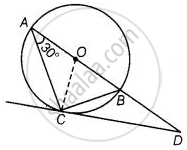
Proof: OA = OC ...[Radii of same circle]
∠OCA = ∠OAC = 30° ...[Angles opposite to equal sides are equal]
∠ACB = 90° ...[Angle in a semicircle is a right angle]
∠OCA + ∠OCB = 90°
30° + ∠OCB = 90°
∠OCB = 60° ...[1]
OC = OB ...[Radii of same circle]
∠OBC = ∠OCB = 60° ...[Angles opposite to equal sides are equal]
Now, ∠OBC + ∠CBD = 180° ...[Linear pair]
60 + ∠CBD = 180°
So, ∠CBD = 120° ...[2]
Also, OC ⊥ CD ...[Tangent at a point on the circle is perpendicular to the radius through point of contact]
∠OCD = 90°
∠OCB + ∠BCD = 90°
60 + ∠BCD = 90
∠BCD = 30° ...[3]
In ΔBCD
∠CBD + ∠BCD + ∠BDC = 180° ...[Angle sum property of triangle]
120° + 30° + ∠BDC = 180° ...[From 2 and 3]
∠BDC = 30° ...[4]
From [3] and [4]
∠BCD = ∠BDC = 30°
BC = BD ...[Sides opposite to equal angles are equal]
Hence proved.
APPEARS IN
RELATED QUESTIONS
A quadrilateral is drawn to circumscribe a circle. Prove that the sums of opposite sides are equal ?
In the given figure, if chords AB and CD of the circle intersect each other at right angles, then x + y =
In the given figure, if ∠ABC = 45°, then ∠AOC =
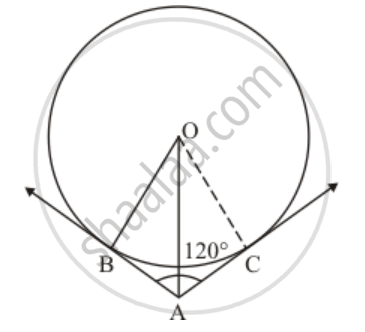
In the given figure, two tangents AB and AC are drawn to a circle with centre O such that ∠BAC = 120°. Prove that OA = 2AB.
Mark two points A and B ,4cm a part, Draw a circle passing through B and with A as a center
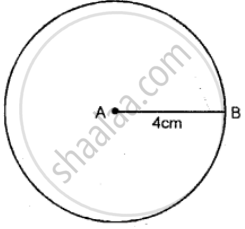
Draw circle with the radii given below.
4 cm
In the given figure, AB is the diameter of the circle. Find the value of ∠ACD.
In figure, tangents PQ and PR are drawn to a circle such that ∠RPQ = 30°. A chord RS is drawn parallel to the tangent PQ. Find the ∠RQS.
[Hint: Draw a line through Q and perpendicular to QP.]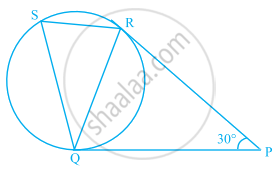
The circumcentre of the triangle ABC is O. Prove that ∠OBC + ∠BAC = 90º.
If an are subtends an angle of 90° at the centre of a circle, then the ratio of its length to the circumference of the circle is ______.
