Advertisements
Advertisements
प्रश्न
AB is a diameter of a circle and AC is its chord such that ∠BAC = 30°. If the tangent at C intersects AB extended at D, then BC = BD.
विकल्प
True
False
उत्तर
This statement is True.
Explanation:
Given: AB is a diameter of circle with center O and AC is a chord such that ∠BAC = 30°
Also tangent at C intersects AB extends at D.
To prove: BC = BD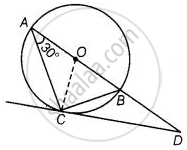
Proof: OA = OC ...[Radii of same circle]
∠OCA = ∠OAC = 30° ...[Angles opposite to equal sides are equal]
∠ACB = 90° ...[Angle in a semicircle is a right angle]
∠OCA + ∠OCB = 90°
30° + ∠OCB = 90°
∠OCB = 60° ...[1]
OC = OB ...[Radii of same circle]
∠OBC = ∠OCB = 60° ...[Angles opposite to equal sides are equal]
Now, ∠OBC + ∠CBD = 180° ...[Linear pair]
60 + ∠CBD = 180°
So, ∠CBD = 120° ...[2]
Also, OC ⊥ CD ...[Tangent at a point on the circle is perpendicular to the radius through point of contact]
∠OCD = 90°
∠OCB + ∠BCD = 90°
60 + ∠BCD = 90
∠BCD = 30° ...[3]
In ΔBCD
∠CBD + ∠BCD + ∠BDC = 180° ...[Angle sum property of triangle]
120° + 30° + ∠BDC = 180° ...[From 2 and 3]
∠BDC = 30° ...[4]
From [3] and [4]
∠BCD = ∠BDC = 30°
BC = BD ...[Sides opposite to equal angles are equal]
Hence proved.
APPEARS IN
संबंधित प्रश्न
Prove that there is one and only one tangent at any point on the circumference of a circle.
Write True or False. Give reason for your answer.
Sector is the region between the chord and its corresponding arc.
Fill in the blank
Circles having the same centre and different radii are called ...........................circles.
In fig. 3 are two concentric circles of radii 6 cm and 4 cm with centre O. If AP is a tangent to the larger circle and BP to the smaller circle and length of AP is 8 cm, find the length of BP ?

If ABCD is a cyclic quadrilateral in which AD || BC (In the given figure). Prove that ∠B = ∠C.

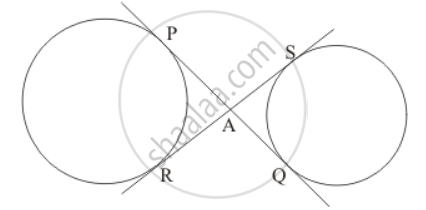
In the given figure, common tangents PQ and RS to two circles intersect at A. Prove that PQ = RS.
ABC is a right triangle in which ∠B = 90°. If AB = 8 cm and BC = 6 cm, find the diameter of the circle inscribed in the triangle.
If a number of circles touch a given line segment PQ at a point A, then their centres lie on the perpendicular bisector of PQ.
If AOB is a diameter of a circle and C is a point on the circle, then AC2 + BC2 = AB2.
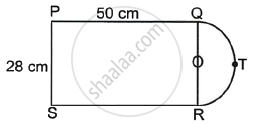
A figure is in the form of rectangle PQRS having a semi-circle on side QR as shown in the figure. Determine the area of the plot.