Advertisements
Advertisements
प्रश्न
ABC is a right triangle in which ∠B = 90°. If AB = 8 cm and BC = 6 cm, find the diameter of the circle inscribed in the triangle.
उत्तर
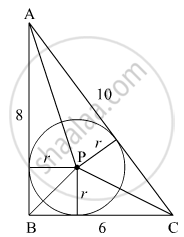
We have given that a circle is inscribed in a triangle
Using pythagoras theorem
`(AC)^2 = (AB)^2 + (BC)^2`
`(AC)^2 = (8)^2 + (6)^2`
`(AC)^2 = 64 + 36`
`(AC)^2 = 100`
⇒ AC = 10
Area of Δ ABC = area of Δ APB + area of Δ BPC + area of Δ APC
`1/2 xx b xx h = 1/2 xx b_1 xx h_1 + 1/2 xx b_2 xx h_2 + 1/2 xx b_3 xx h_3`
`1/2 xx 6 xx 8 = 1/2 xx 8 xx r + 1/2 xx 6 xx r + 1/2 xx 10 xx r`
`24 = 4r + 3r + 5r`
`24 = 12r`
⇒ r = 2
∵ d = 2r
⇒ `d = 2 xx 2`
⇒ d = 4 cm
APPEARS IN
संबंधित प्रश्न
In Fig. 2, AB is the diameter of a circle with centre O and AT is a tangent. If ∠AOQ = 58°, find ∠ATQ.

Two tangent segments PA and PB are drawn to a circle with center O such that ∠APB =120°. Prove that OP = 2AP
From an external point P, tangents PA and PB are drawn to a circle with center O. If CD is the tangent to the circle at a point E and PA = 14cm, find the perimeter of ΔPCD.

In Fig. 4, an isosceles triangle ABC, with AB = AC, circumscribes a circle. Prove that the point of contact P bisects the base BC.
An equilateral triangle ABC is inscribed in a circle with centre O. The measures of ∠BOCis
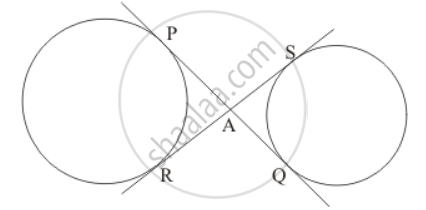
In the given figure, common tangents PQ and RS to two circles intersect at A. Prove that PQ = RS.
Choose correct alternative answer and fill in the blank.
Radius of a circle is 10 cm and distance of a chord from the centre is 6 cm. Hence the length of the chord is .........
Construct a triangle PQR with QR = 5.5 cm, ∠Q = 60° and angle R = 45°. Construct the circumcircle cif the triangle PQR.
In the figure, O is the centre of the circle, and ∠AOB = 90°, ∠ABC = 30°. Then find ∠CAB.

From the figure, identify three radii.