Advertisements
Advertisements
प्रश्न
Out of the two concentric circles, the radius of the outer circle is 5 cm and the chord AC of length 8 cm is a tangent to the inner circle. Find the radius of the inner circle.
उत्तर
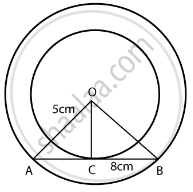
From the figure,
Chord AB = 8 cm
OC is perpendicular to the chord AB
AC = CB = 4 cm
In right triangle OCA
OC2 + CA2 = OA2
OC2 = 52 – 42
= 25 – 16
= 9
OC = 3 cm
संबंधित प्रश्न
How many tangents can a circle have?
A circle touches all the four sides of a quadrilateral ABCD. Prove that AB + CD = BC + DA.
In the given figure AC is a tangent to the circle with centre O.
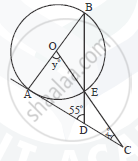
If ∠ADB = 55° , find x and y. Give reasons for your answers.
In the given figure, O is the centre of the circle. Tangents at A and B meet at C. If angle ACO = 30°, find: angle APB

In figure, if ∠AOB = 125°, then ∠COD is equal to ______.
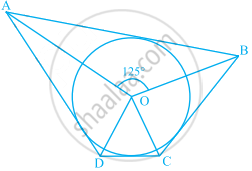
In Question 5 above, if radii of the two circles are equal, prove that AB = CD.
Construct a pair of tangents to a circle of radius 4 cm, which are inclined to each other at an angle of 60°.
In the given figure, PA is a tangent to the circle drawn from the external point P and PBC is the secant to the circle with BC as diameter. If ∠AOC = 130°, then find the measure of ∠APB, where O is the centre of the circle.

In the given figure, PT is a tangent at T to the circle with centre O. If ∠TPO = 25°, then x is equal to ______.

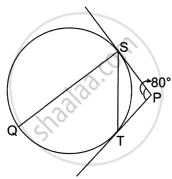
In the given diagram, PS and PT are the tangents to the circle. SQ || PT and ∠SPT = 80°. The value of ∠QST is ______.