Advertisements
Advertisements
प्रश्न
A circle touches all the four sides of a quadrilateral ABCD. Prove that AB + CD = BC + DA.
उत्तर
ABCD is a quadrilateral. Suppose a circle touches the sides AB, BC, CD and DA of the quadrilateral ABCD at P, Q, R and S, respectively.
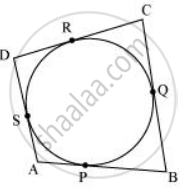
We know that the length of tangents drawn from an external point to a circle are equal.
DR = DS ...(1)
CR = CQ ...(2)
BP = BQ ...(3)
AP = AS ...(4)
Adding (1), (2), (3) and (4), we get
DR + CR + BP + AP = DS + CQ + BQ + AS
(DR + CR) + (BP + AP) = (DS + AS) + (CQ + BQ)
CD + AB = AD + BC
Or, AB + CD = BC + DA
APPEARS IN
संबंधित प्रश्न
Draw a circle of radius 3.5 cm. Marks a point P outside the circle at a distance of 6 cm from the centre. Construct two tangents from P to the given circle. Measure and write down the length of one tangent.
A chord PQ of a circle is parallel to the tangent drawn at a point R of the circle. Prove that R bisects the arc PRQ.
Prove that a diameter AB of a circle bisects all those chords which are parallel to the tangent at the point A.
Two chords AB and CD of lengths 6cm and 12cm are drawn parallel inside the circle. If the distance between the chords of the circle is 3cm, find the radius of the circle.
Calculate the length of direct common tangent to two circles of radii 3cm and Bern with their centres 13cm apart.
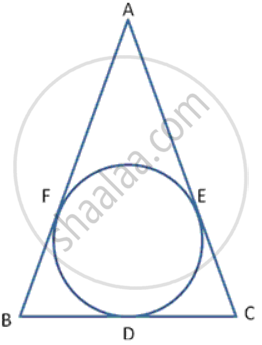
In following figure , the incircle of Δ ABC , touches the sides BC , CA and AB at D , E and F respectively. Show AF + BD + CE = AE + BF + CD
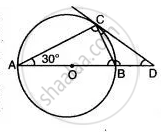
In Figure, AB is diameter and AC is a chord of a circle such that ∠BAC = 30°. The tangent at C intersects AB produced at D. Prove that BC = BD.
In figure, AT is a tangent to the circle with centre O such that OT = 4 cm and ∠OTA = 30°. Then AT is equal to ______.

Two parallel lines touch the circle at
points A and B respectively. If the area of the circle is 25 n cm2, then AB is equal to ______
In the given diagram an isosceles ΔABC is inscribed in a circle with centre O. PQ is a tangent to the circle at C. OM is perpendicular to chord AC and ∠COM = 65°.

Find:
- ∠ABC
- ∠BAC
- ∠BCQ
