Advertisements
Advertisements
Question
A circle touches all the four sides of a quadrilateral ABCD. Prove that AB + CD = BC + DA.
Solution
ABCD is a quadrilateral. Suppose a circle touches the sides AB, BC, CD and DA of the quadrilateral ABCD at P, Q, R and S, respectively.
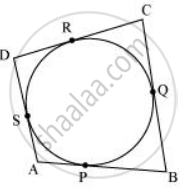
We know that the length of tangents drawn from an external point to a circle are equal.
DR = DS ...(1)
CR = CQ ...(2)
BP = BQ ...(3)
AP = AS ...(4)
Adding (1), (2), (3) and (4), we get
DR + CR + BP + AP = DS + CQ + BQ + AS
(DR + CR) + (BP + AP) = (DS + AS) + (CQ + BQ)
CD + AB = AD + BC
Or, AB + CD = BC + DA
APPEARS IN
RELATED QUESTIONS
Prove that the tangent drawn at the mid-point of an arc of a circle is parallel to the chord joining the end points of the arc.
ABC is a right triangle with angle B = 90º. A circle with BC as diameter meets by hypotenuse AC at point D. Prove that: BD2 = AD × DC.
Construct a tangent to a circle with centre O and radius 3.5 cm at a point P on it.
Find the area of sector whose central angle and radius are 60o and 21 cm respectively.
`(pi = 22/7)`
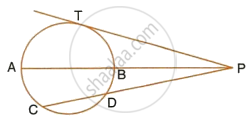
In the given figure, diameter AB and chord CD of a circle meet at P. PT is a tangent to the circle at T. CD = 7.8 cm, PD = 5 cm, PB = 4 cm. Find:
- AB.
- the length of tangent PT.
The tangents drawn at the extremities of the diameter of a circle are ______.
In Question 5 above, if radii of the two circles are equal, prove that AB = CD.
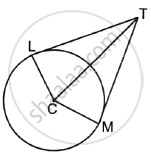
If two tangents TL and TM are drawn to a circle with centre C such that ∠LTM = 70°, then find ∠MCT.
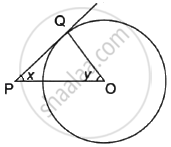
In the given figure, PQ is a tangent to the circle with centre O. If ∠OPQ = x, ∠POQ = y, then x + y is ______.
The length of tangent drawn to a circle of radius 9 cm from a point 41 cm from the centre is ______.
