Advertisements
Advertisements
Question
In Question 5 above, if radii of the two circles are equal, prove that AB = CD.
Solution
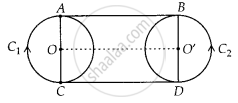
Join OO’
Since, OA = O’B ...[Given]
Also, ∠OAB = ∠O’BA = 90° ...[Tangent at any point of a circle is perpendicular to the radius at the point of contact]
Since, perpendicular distance between two straight lines at two different points is same.
⇒ AB is parallel to OO’
Similarly, CD is parallel to OO’
⇒ AB ॥ CD
Also, ∠OAB = ∠OCD = ∠O’BA = ∠O’DC = 90°
⇒ ABCD is a rectangle.
Hence, AB = CD.
APPEARS IN
RELATED QUESTIONS
A chord PQ of a circle is parallel to the tangent drawn at a point R of the circle. Prove that R bisects the arc PRQ.
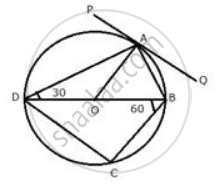
In the following figure, PQ is the tangent to the circle at A, DB is a diameter and O is the centre of the circle. If ∠ ADB = 30° and ∠ CBD = 60° ; calculate ∠ PAD.
In the given figure, O is the centre of the circle. Tangents at A and B meet at C. If angle ACO = 30°, find: angle APB

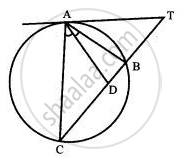
In Fig. TA is a tangent to a circle from the point T and TBC is a secant to the circle. If AD is the bisector of ∠BAC, prove that ΔADT is isosceles.
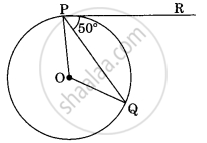
In figure, if O is the centre of a circle PQ is a chord and the tangent PR at P makes an angle of 50° with PQ, then ∠POQ is equal to ______.
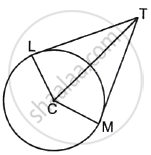
If two tangents TL and TM are drawn to a circle with centre C such that ∠LTM = 70°, then find ∠MCT.
A tangent JK is drawn to a circle with centre C such that CK = 6 cm and ∠CKJ = 60°. Find the length of the tangent JK.

Assertion (A): A tangent to a circle is perpendicular to the radius through the point of contact.
Reason (R): The lengths of tangents drawn from an external point to a circle are equal.

In the given figure, QR is a common tangent to the two given circles touching externally at A. The tangent at A meets QR at P. If AP = 4.2 cm, then the length of QR is ______.
In the given diagram an isosceles ΔABC is inscribed in a circle with centre O. PQ is a tangent to the circle at C. OM is perpendicular to chord AC and ∠COM = 65°.
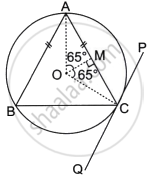
Find:
- ∠ABC
- ∠BAC
- ∠BCQ
