Advertisements
Advertisements
Question
In the given figure, O is the centre of the circle. Tangents at A and B meet at C. If angle ACO = 30°, find: angle APB

Solution
In the given fig, O is the centre of the circle and CA and CB are the tangents to the circle from C. Also, ∠ ACO = 30°
P is any point on the circle. P and PB are joined.
To find : ∠ APB
Proof :
Arc AB subtends ∠ AOB at the centre and ∠ APB
is in the remaining part of the circle.
∴ `∠ "APB" = 1/2 ∠ "AOB" =1/2 xx120 = 60°`
APPEARS IN
RELATED QUESTIONS
In the given figure, find TP if AT = 16 cm and AB = 12 cm.

In Figure 2, XP and XQ are two tangents to the circle with centre O, drawn from an external point X. ARB is another tangent, touching the circle at R. Prove that XA + AR = XB + BR ?

In the adjoining figure the radius of a circle with centre C is 6 cm, line AB is a tangent at A. Answer the following questions.
(1) What is the measure of ∠CAB ? Why ?
(2) What is the distance of point C from line AB? Why ?
(3) d(A,B) = 6 cm, find d(B,C).
(4) What is the measure of ∠ABC ? Why ? 

In the figure, point Q is the
point of contact. If PQ = 12,
PR = 8 then find PS.
In the given figure, diameter AB and chord CD of a circle meet at P. PT is a tangent to the circle at T. CD = 7.8 cm, PD = 5 cm, PB = 4 cm. Find the length of tangent PT.

In the following figure, PQ is the tangent to the circle at A, DB is a diameter and O is the centre of the circle. If ∠ ADB = 30° and ∠ CBD = 60° ; calculate : ∠CDB

Find the value of ∠DCE.

ABCD is a cyclic quadrilateral PQ is a tangent at B. If ∠DBQ = 65°, then ∠BCD is ______

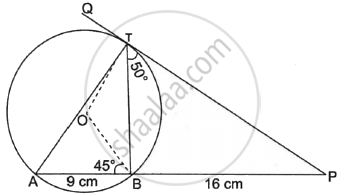
In the given figure, O is the centre of the circle. PQ is a tangent to the circle at T. Chord AB produced meets the tangent at P.
AB = 9 cm, BP = 16 cm, ∠PTB = 50° ∠OBA = 45°
Find:
- Length of PT
- ∠BAT
- ∠BOT
- ∠ABT
In the given figure O, is the centre of the circle. CE is a tangent to the circle at A. If ∠ABD = 26° find:
- ∠BDA
- ∠BAD
- ∠CAD
- ∠ODB

