Advertisements
Advertisements
Question
ABC is a triangle with AB = 10 cm, BC = 8 cm and AC = 6 cm (not drawn to scale). Three circle are drawn touching each other with the vertices as their centres. Find the radii of the three circles.
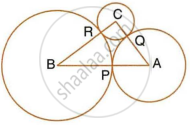
Solution
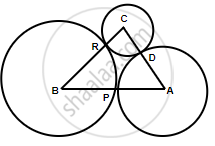
Given: ABC is a triangle with AB = 10 cm, BC = 8 cm, AC = 6 cm. Three circles are drawn with centre A, B and C touch each other at P, Q and R respectively.
We need to find the radii of the three circles.
Let
PA = AQ = x
QC = CR = y
RB = BP = z
∴ x + z = 10 ...(1)
z + y = 8 ...(2)
y + x = 6 ...(3)
Adding all the three equations, we have
2(x + y + z) = 24
`=> x + y + z = 24/2 = 12` ...(4)
Subtracting (1) (2) and (3) from (4)
y = 12 – 10 = 2
x = 12 – 8 = 4
z = 12 – 6 = 6
Therefore, radii are 2 cm, 4 cm and 6 cm
APPEARS IN
RELATED QUESTIONS
Three circles touch each other externally. A triangle is formed when the centres of these circles are joined together. Find the radii of the circle, if the sides of the triangle formed are 6 cm, 8 cm and 9 cm.
The line joining the mid-points of two chords of a circle passes through its centre. Prove that the
chords are parallel.
