Advertisements
Advertisements
Question
In a square ABCD, its diagonals AC and BD intersect each other at point O. The bisector of angle DAO meets BD at point M and the bisector of angle ABD meets AC at N and AM at L. Show that:
- ∠ONL + ∠OML = 180°
- ∠BAM + ∠BMA
- ALOB is a cyclic quadrilateral.
Solution
ABCD is a square whose diagonals AC and BD intersect each other at right angles at O.
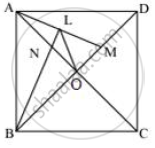
i. ∴ ∠AOB = ∠AOD = 90°
In ΔANB,
∠ANB = 180° – (∠NAB + ∠NBA)
`=>` `∠ANB = 180^circ - (45^circ + (45^circ)/2)` ...(NB is bisector of ∠ABD)
`=> ∠ANB = 180^circ - 45^circ - 45^circ/2 = 135^circ - 45^circ/2`
But, ∠LNO = ∠ANB ...(Vertically opposite angles)
∴ `∠LNO = 135^circ - 45^circ/2` ...(i)
Now in ΔAMO,
∠AMO = 180° – (∠AOM + ∠OAM)
`=> ∠AMO = 180^circ - (90^circ + (45^circ)/2)` ...(MA is bisector of ∠DAO)
`=>∠AMO = 180^circ - 90^circ - (45^circ)/2 = 90^circ - (45^circ)/2` ...(ii)
Adding (i) and (ii)
`∠LNO + ∠AMO = 135^circ - 45^circ/2 + 90^circ - 45^circ/2`
`=>` ∠LNO + ∠AMO = 225° – 45° = 180°
`=>` ∠ONL + ∠OML = 180°
ii. ∠BAM = ∠BAO + ∠OAM
`=> ∠BAM = 45^circ + (45^circ)/2 = 67 1^circ/2`
And
`=>` ∠BMA = 180° – (∠AOM + ∠OAM)
`=> ∠BMA = 180^circ - 90^circ - 45^circ/2`
= `90^circ - 45^circ/2`
= `67 1^circ/2`
∴ ∠BAM = ∠BMA
iii. In quadrilateral ALOB,
∵ ∠ABO + ∠ALO = 45° + 90° + 45° = 180°
Therefore, ALOB is a cyclic quadrilateral.
APPEARS IN
RELATED QUESTIONS
In the given figure, SP is bisector of ∠RPT and PQRS is a cyclic quadrilateral. Prove that : SQ = SR.

In the following figure, ABCD is a cyclic quadrilateral in which AD is parallel to BC.
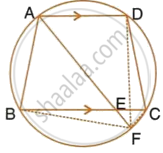
If the bisector of angle A meets BC at point E and the given circle at point F, prove that:
- EF = FC
- BF = DF
ABCD is a cyclic quadrilateral. Sides AB and DC produced meet at point E; whereas sides BC and AD produced meet at point F. If ∠DCF : ∠F : ∠E = 3 : 5 : 4, find the angles of the cyclic quadrilateral ABCD.
Prove that any four vertices of a regular pentagon are concylic (lie on the same circle).
In the given below the figure, O is the centre of the circle and ∠ AOC = 160°. Prove that 3∠y - 2∠x = 140°.

The diagonals of a cyclic quadrilateral are at right angles. Prove that the perpendicular from the point of their intersection on any side when produced backward bisects the opposite side.
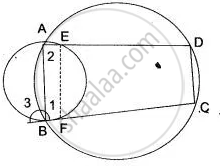
In Fig. ABCD is a cyclic quadrilateral. A circle passing through A and B meets AD and BC in the points E and F respectively. Prove that EF || DC.
In the given below figure,
∠ BAD = 65°
∠ ABD = 70°
∠ BDC = 45°
Find: (i) ∠ BCD, (ii) ∠ ADB.
Hence show that AC is a diameter.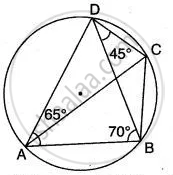
In the figure , Δ PQR is an isosceles triangle with PQ = PR, and m ∠ PQR = 35°. Find m ∠ QSR and ∠ QTR.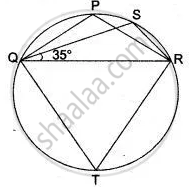
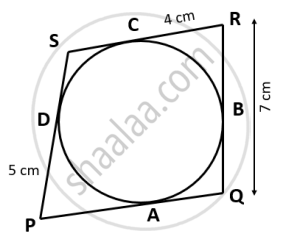
In the given figure, the sides of the quadrilateral PQRS touches the circle at A, B, C and D. If RC = 4 cm, RQ = 7 cm and PD = 5 cm. Find the length of PQ: