Advertisements
Advertisements
Question
In the given below figure,
∠ BAD = 65°
∠ ABD = 70°
∠ BDC = 45°
Find: (i) ∠ BCD, (ii) ∠ ADB.
Hence show that AC is a diameter.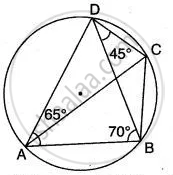
Solution
Given:
∠ BAD = 65°
∠ ABD = 70°
∠ BDC = 45°
(i) Quadrilateral ABCD is cyclic quadrilateral.
∴ ∠ DAB + ∠ BCD = 180°
∴ 65° + ∠ BCD = 180°
∴ ∠ BCD = 180° - 65°
∴ ∠ BCD = 115°
(ii) In ΔADB,
∴ ∠ DAB + ∠ ABD + ∠ ADB = 180°
∴ 65° + 70° + ∠ ADB = 180°
∴ ∠ ADB = 180° - 135°
∴ ∠ ADB = 45°.
APPEARS IN
RELATED QUESTIONS
In the figure given, O is the centre of the circle. ∠DAE = 70°. Find giving suitable reasons, the measure of:
- ∠BCD
- ∠BOD
- ∠OBD

ABCD is a cyclic quadrilateral in a circle with centre O. If ∠ADC = 130°; find ∠BAC.

D and E are points on equal sides AB and AC of an isosceles triangle ABC such that AD = AE. Prove that the points B, C, E and D are concyclic.
ABCD is a cyclic quadrilateral. Sides AB and DC produced meet at point E; whereas sides BC and AD produced meet at point F. If ∠DCF : ∠F : ∠E = 3 : 5 : 4, find the angles of the cyclic quadrilateral ABCD.
Prove that any four vertices of a regular pentagon are concylic (lie on the same circle).
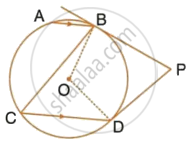
In the given figure, O is the centre of the circle. The tangents at B and D intersect each other at point P. If AB is parallel to CD and ∠ABC = 55°, find:
- ∠BOD
- ∠BPD
In a cyclic quadrilateral ABCD , AB || CD and ∠ B = 65° , find the remaining angles.
In a cyclic quadrialteral ABCD , if m ∠ A = 3 (m ∠C). Find m ∠ A.
Prove that the angles bisectors of the angles formed by producing opposite sides of a cyclic quadrilateral (provided they are not parallel) intersect at right triangle.
Prove that the angle bisectors of the angles formed by producing opposite sides of a cyclic quadrilateral (Provided they are not parallel) intersect at the right angle.
