Advertisements
Advertisements
Question
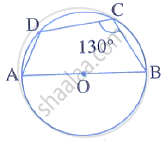
ABCD is a cyclic quadrilateral in a circle with centre O. If ∠ADC = 130°; find ∠BAC.

Solution

Here ∠ACB = 90°
(Angle in a semicircle is right angle)
Also, ∠ABC = 180° – ∠ADC = 180° – 130° = 50°
(Pair of opposite angles in a cyclic quadrilateral are supplementary)
By angle sum property of right triangle ACB,
∠BAC = 90° – ∠ABC = 90° – 50° = 40°
APPEARS IN
RELATED QUESTIONS
ABCD is a cyclic quadrilateral in which BC is parallel to AD, angle ADC = 110° and angle BAC = 50°. Find angle DAC and angle DCA.
In the given figure, AB is the diameter of a circle with centre O. ∠BCD = 130°. Find:
(i) ∠DAB
(ii) ∠DBA
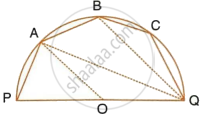
The given figure shows a semi-circle with centre O and diameter PQ. If PA = AB and ∠BCQ =140°; find measures of angles PAB and AQB. Also, show that AO is parallel to BQ.
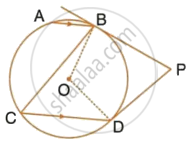
In the given figure, O is the centre of the circle. The tangents at B and D intersect each other at point P. If AB is parallel to CD and ∠ABC = 55°, find:
- ∠BOD
- ∠BPD
In following figure , O is the centre of the circle. If ∠ APB = 50° then find ∠ AOB and ∠ OAB.

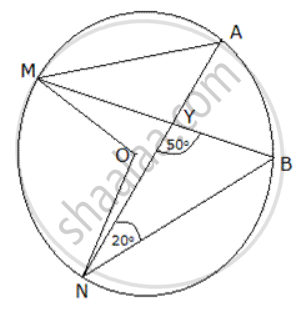
MABN are points on a drde having centre O. AN and MB cut at Y. If ∠ NYB = 50" and ∠ YNB = 200, find ∠ MAN and reflex angle MON.
In the figure, ∠DBC = 58°. BD is a diameter of the circle. Calculate : ∠BAC
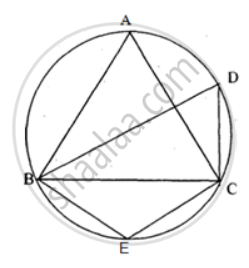
Prove that the angle bisectors of the angles formed by producing opposite sides of a cyclic quadrilateral (Provided they are not parallel) intersect at the right angle.
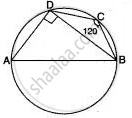
In the adjoining figure, AB is the diameter of the circle with centre O. If ∠BCD = 120°, calculate:
(i) ∠BAD (ii) ∠DBA
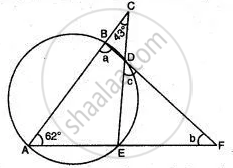
In the given figure, if ∠ ACE = 43° and ∠CAF = 62°. Find the value of a, b, and c.