Advertisements
Advertisements
Question
The given figure shows a semi-circle with centre O and diameter PQ. If PA = AB and ∠BCQ =140°; find measures of angles PAB and AQB. Also, show that AO is parallel to BQ.
Solution
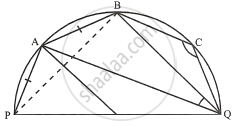
Join PB.
i. In cyclic quadrilateral PBCQ,
∠BPQ + ∠BCQ = 180°
Now in ΔPBQ,
∠PBQ + ∠BPQ + ∠BQP = 180°
In cyclic quadrilateral PQBA,
∠PQB + ∠PAB = 180°
ii. Now in ΔPAB,
∠PAB + ∠APB + ∠ABP = 180°
But ∠APB = ∠ABP ...(∵ PA = PB)
∴ ∠APB = ∠ABP = 25°
∠BAQ = ∠BPQ = 40°
∠APB = 25° = ∠AQB ...(Angles in the same segment)
∴ ∠AQB = 25° ...(2)
iii. Arc AQ subtends ∠AOQ at the centre and ∠APQ at the remaining part of the circle.
We have,
∠APQ = ∠APB + ∠BPQ ...(3)
From (1), (2) and (3), we have
∠APQ = 25° + 40° = 65°
∴ ∠AOQ = 2∠APQ = 2 × 65° = 130°
Now in ΔAOQ,
∠OAQ = ∠OQA ...( ∵ OA = OQ)
But ∠OAQ + ∠OQA + ∠AOQ = 180°
∴ ∠OAQ = ∠AQB
But these are alternate angles.
Hence, AO is parallel to BQ.
APPEARS IN
RELATED QUESTIONS
In the given figure, AB = AC. Prove that DECB is an isosceles trapezium.
In a cyclic-quadrilateral PQRS, angle PQR = 135°. Sides SP and RQ produced meet at point A whereas sides PQ and SR produced meet at point B. If ∠A : ∠B = 2 : 1; find angles A and B.
In the given figure, PAT is tangent to the circle with centre O at point A on its circumference and is parallel to chord BC. If CDQ is a line segment, show that:
- ∠BAP = ∠ADQ
- ∠AOB = 2∠ADQ
- ∠ADQ = ∠ADB

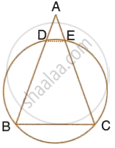
The bisectors of the opposite angles A and C of a cydic quadrilateral ABCD intersect the cirde at the points E and F, respectively. Prove that EF is a diameter of the circle.
Bisectors of angles A, B and C of a triangle ABC intersect its circumcircle at D, E and F respectively. Prove that the angles of Δ DEF are 90° -
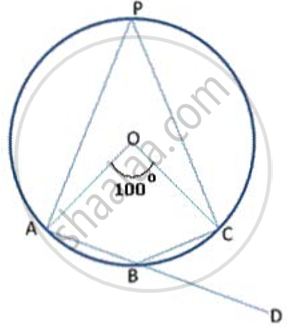
In following fig., O is the centre of the circle. Find ∠ CBD.
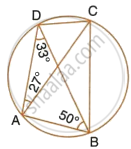
In cyclic quadrilateral ABCD, ∠DAC = 27°; ∠DBA = 50° and ∠ADB = 33°. Calculate : ∠DCB.
In the given below the figure, O is the centre of the circle and ∠ AOC = 160°. Prove that 3∠y - 2∠x = 140°.

If ABCD is a cyclic quadrilateral in which AD || BC. Prove that ∠B = ∠C.
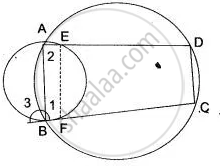
In Fig. ABCD is a cyclic quadrilateral. A circle passing through A and B meets AD and BC in the points E and F respectively. Prove that EF || DC.