Advertisements
Advertisements
Question
In a cyclic-quadrilateral PQRS, angle PQR = 135°. Sides SP and RQ produced meet at point A whereas sides PQ and SR produced meet at point B. If ∠A : ∠B = 2 : 1; find angles A and B.
Solution
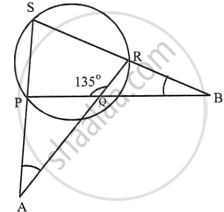
PQRS is a cyclic quadrilateral in which ∠PQR = 135°
Sides SP and RQ are produced to meet at A and sides PQ and SR are produced to meet at B.
∠A : ∠B = 2 : 1
Let ∠A = 2x, then ∠B = x
Now, in cyclic quad PQRS,
Since, ∠PQR = 135°, ∠S = 180° – 135° = 45°
[Since sum of opposite angles of a cyclic quadrilateral are supplementary]
Since, ∠PQR and ∠PQA are linear pair,
∠PQR + ∠PQA = 180°
`=>` 135° + ∠PQA = 180°
`=>` ∠PQA = 180° – 135° = 45°
Now, In ∆PBS,
∠P = 180° – (45° + x)
= 180° – 45° – x
= 135° – x ...(1)
Again, in ∆PQA,
EXT ∠P = ∠PQA + ∠A
= 45° + 2x ...(2)
From (1) and (2),
45° + 2x = 135° – x
`=>` 2x + x = 135° – 45°
`=>` 3x = 90°
`=>` x = 30°
Hence, ∠A = 2x = 2 × 30° = 60° and ∠B = x = 30°
APPEARS IN
RELATED QUESTIONS
In a cyclic quadrilateral ABCD, the diagonal AC bisects the angle BCD. Prove that the diagonal BD is parallel to the tangent to the circle at point A.
In the given figure, SP is bisector of ∠RPT and PQRS is a cyclic quadrilateral. Prove that : SQ = SR.

Bisectors of vertex angles A, B, and C of a triangle ABC intersect its circumcircle at the points D, E and F respectively. Prove that angle EDF = 90° – `1/2` ∠A.
In a cyclic quadrilateral ABCD, ∠A : ∠C = 3 : 1 and ∠B : ∠D = 1 : 5; find each angle of the quadrilateral.
ABCDE is a cyclic pentagon with centre of its circumcircle at point O such that AB = BC = CD and angle ABC = 120°.
Calculate:
- ∠BEC
- ∠BED
In following figure , O is the centre of the circle. If ∠ APB = 50° then find ∠ AOB and ∠ OAB.

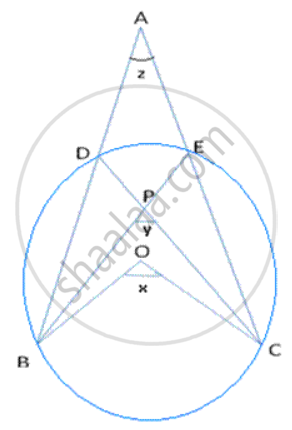
In following fig., O is the centre of the circle, prove that ∠x =∠ y + ∠ z.
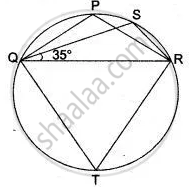
In following figure , Δ PQR is an isosceles teiangle with PQ = PR and m ∠ PQR = 35° .Find m ∠ QSR and ∠ QTR

In the given figure O is the center of the circle, ∠ BAD = 75° and chord BC = chord CD. Find:
(i) ∠BOC (ii) ∠OBD (iii) ∠BCD.
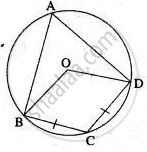
In the figure , Δ PQR is an isosceles triangle with PQ = PR, and m ∠ PQR = 35°. Find m ∠ QSR and ∠ QTR.