Advertisements
Advertisements
Question
In a cyclic quadrilateral ABCD, the diagonal AC bisects the angle BCD. Prove that the diagonal BD is parallel to the tangent to the circle at point A.
Solution
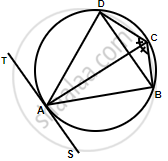
∠ADB = ∠ACB ...(i) (Angles in same segement)
Similarly,
∠ABD = ∠ACD ...(ii)
But, ∠ACB = ∠ACD ...(AC is bisector of ∠BCD)
∴ ∠ADB = ∠ABD ...(From (i) and (ii))
TAS is a tangent and AB is a chord
∴ ∠BAS = ∠ADB ...(Angles in alternate segment)
But, ∠ADB = ∠ABD
∴ ∠BAS = ∠ABD
But these are alternate angles
Therefore, TS || BD
APPEARS IN
RELATED QUESTIONS
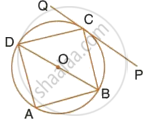
In the given figure, ABCD is a cyclic quadrilateral, PQ is tangent to the circle at point C and BD is its diameter. If ∠DCQ = 40° and ∠ABD = 60°, find;
- ∠DBC
- ∠BCP
- ∠ADB
D and E are points on equal sides AB and AC of an isosceles triangle ABC such that AD = AE. Prove that the points B, C, E and D are concyclic.
In a cyclic-quadrilateral PQRS, angle PQR = 135°. Sides SP and RQ produced meet at point A whereas sides PQ and SR produced meet at point B. If ∠A : ∠B = 2 : 1; find angles A and B.
In a cyclic quadrilateral ABCD , AB || CD and ∠ B = 65° , find the remaining angles.
In a circle with centre O , chords AB and CD intersets inside the circle at E . Prove that ∠ AOC = ∠ BOD = 2 ∠ AEC.
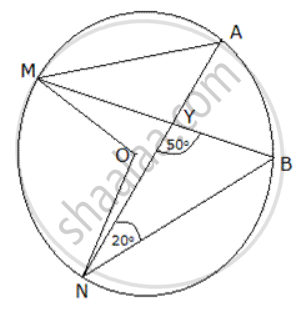
MABN are points on a drde having centre O. AN and MB cut at Y. If ∠ NYB = 50" and ∠ YNB = 200, find ∠ MAN and reflex angle MON.
In following figure , Δ PQR is an isosceles teiangle with PQ = PR and m ∠ PQR = 35° .Find m ∠ QSR and ∠ QTR

ABCDE is a cyclic pentagon with centre of its circumcircle at point O such that AB = BC = CD and angle ABC=120°.
Calculate: ∠ BED.
ABCD is a cyclic quadrilateral AB and DC are produced to meet in E. Prove that Δ EBC ∼ Δ EDA.
An exterior angle of a cyclic quadrilateral is congruent to the angle opposite to its adjacent interior angle, to prove the theorem complete the activity.
Given: ABCD is cyclic,
`square` is the exterior angle of ABCD
To prove: ∠DCE ≅ ∠BAD
Proof: `square` + ∠BCD = `square` .....[Angles in linear pair] (I)
ABCD is a cyclic.
`square` + ∠BAD = `square` ......[Theorem of cyclic quadrilateral] (II)
By (I) and (II)
∠DCE + ∠BCD = `square` + ∠BAD
∠DCE ≅ ∠BAD
