Advertisements
Advertisements
Question
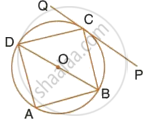
In the given figure, ABCD is a cyclic quadrilateral, PQ is tangent to the circle at point C and BD is its diameter. If ∠DCQ = 40° and ∠ABD = 60°, find;
- ∠DBC
- ∠BCP
- ∠ADB
Solution
i. PQ is tangent and CD is a chord
∴ ∠DCQ = ∠DBC ...(Angles in the alternate segment)
∴ DBC = 40° ...(∵ ∠DCQ = 40°)
ii. ∠DCQ + ∠DCB + ∠BCP = 180°
`=>` 40° + 90° + ∠BCP = 180° ...(∵ ∠DCB = 90°)
`=>` 130° + ∠BCP = 180°
∴ ∠BCP = 180° – 130° = 50°
iii. In ΔABD,
∠BAD = 90°, ∠ABD = 60°
∴ ∠ADB = 180° – (90° + 60°)
`=>` ∠ADB = 180° – 150° = 30°
APPEARS IN
RELATED QUESTIONS
In the given figure, AB is the diameter of a circle with centre O. ∠BCD = 130o. Find:
1) ∠DAB
2) ∠DBA

ABCD is a cyclic quadrilateral in a circle with centre O. If ∠ADC = 130°; find ∠BAC.

In a cyclic quadrilateral ABCD, the diagonal AC bisects the angle BCD. Prove that the diagonal BD is parallel to the tangent to the circle at point A.
Bisectors of vertex angles A, B, and C of a triangle ABC intersect its circumcircle at the points D, E and F respectively. Prove that angle EDF = 90° – `1/2` ∠A.
In the given figure, AB is parallel to DC, ∠BCE = 80° and ∠BAC = 25°.

Find:
- ∠CAD
- ∠CBD
- ∠ADC
In a circle with centre O , chords AB and CD intersets inside the circle at E . Prove that ∠ AOC = ∠ BOD = 2 ∠ AEC.
In following figure , Δ PQR is an isosceles teiangle with PQ = PR and m ∠ PQR = 35° .Find m ∠ QSR and ∠ QTR

Prove that the quadrilateral formed by angle bisectors of a cyclic quadrilateral ABCD is also cyclic.
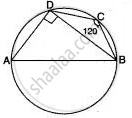
In the adjoining figure, AB is the diameter of the circle with centre O. If ∠BCD = 120°, calculate:
(i) ∠BAD (ii) ∠DBA
An exterior angle of a cyclic quadrilateral is congruent to the angle opposite to its adjacent interior angle, to prove the theorem complete the activity.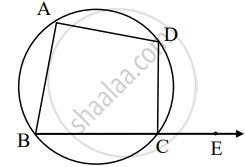
Given: ABCD is cyclic,
`square` is the exterior angle of ABCD
To prove: ∠DCE ≅ ∠BAD
Proof: `square` + ∠BCD = `square` .....[Angles in linear pair] (I)
ABCD is a cyclic.
`square` + ∠BAD = `square` ......[Theorem of cyclic quadrilateral] (II)
By (I) and (II)
∠DCE + ∠BCD = `square` + ∠BAD
∠DCE ≅ ∠BAD
