Advertisements
Advertisements
प्रश्न
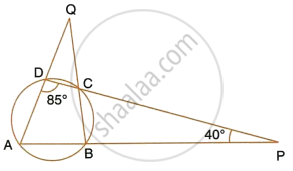
In the given figure, ABCD is a cyclic quadrilateral, PQ is tangent to the circle at point C and BD is its diameter. If ∠DCQ = 40° and ∠ABD = 60°, find;
- ∠DBC
- ∠BCP
- ∠ADB
उत्तर
i. PQ is tangent and CD is a chord
∴ ∠DCQ = ∠DBC ...(Angles in the alternate segment)
∴ DBC = 40° ...(∵ ∠DCQ = 40°)
ii. ∠DCQ + ∠DCB + ∠BCP = 180°
`=>` 40° + 90° + ∠BCP = 180° ...(∵ ∠DCB = 90°)
`=>` 130° + ∠BCP = 180°
∴ ∠BCP = 180° – 130° = 50°
iii. In ΔABD,
∠BAD = 90°, ∠ABD = 60°
∴ ∠ADB = 180° – (90° + 60°)
`=>` ∠ADB = 180° – 150° = 30°
APPEARS IN
संबंधित प्रश्न
In the figure, ABCD is a cyclic quadrilateral with BC = CD. TC is tangent to the circle at point C and DC is produced to point G. If ∠BCG = 108° and O is the centre of the circle, find :
- angle BCT
- angle DOC

In the given figure, SP is bisector of ∠RPT and PQRS is a cyclic quadrilateral. Prove that : SQ = SR.

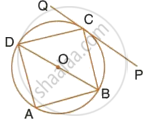
Use the given figure to find:
- ∠BAD,
- ∠DQB.
In a square ABCD, its diagonals AC and BD intersect each other at point O. The bisector of angle DAO meets BD at point M and the bisector of angle ABD meets AC at N and AM at L. Show that:
- ∠ONL + ∠OML = 180°
- ∠BAM + ∠BMA
- ALOB is a cyclic quadrilateral.
In a cyclic quadrilateral ABCD , AB || CD and ∠ B = 65 ° , find the remaining angles
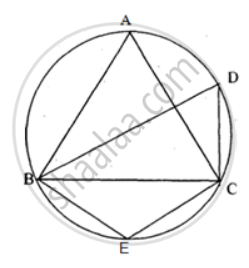
In the figure, ∠DBC = 58°. BD is a diameter of the circle. Calculate : ∠BDC
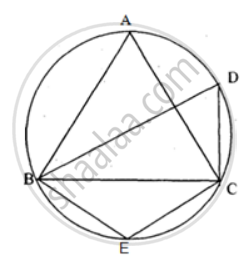
In the figure, ∠DBC = 58°. BD is a diameter of the circle. Calculate : ∠BEC
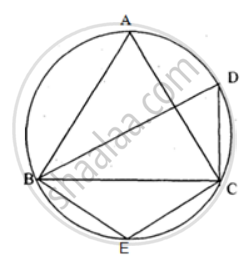
In the figure, ∠DBC = 58°. BD is a diameter of the circle. Calculate : ∠BAC
In the given circle with centre O, ∠ABC = 100°, ∠ACD = 40° and CT is a tangent to the circle at C. Find ∠ADC and ∠DCT.

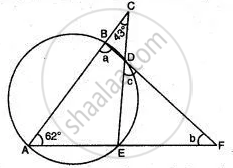
In the given figure, if ∠ ACE = 43° and ∠CAF = 62°. Find the value of a, b, and c.