Advertisements
Advertisements
प्रश्न
In the given figure, SP is bisector of ∠RPT and PQRS is a cyclic quadrilateral. Prove that : SQ = SR.

उत्तर
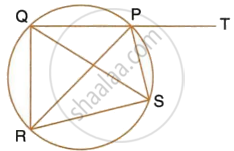
PQRS is a cyclic quadrilateral
∠QRS + ∠QPS = 180° ...(i)
(Pair of opposite angles in a cyclic quadrilateral are supplementary)
Also, ∠QPS + ∠SPT = 180° ...(ii)
(Straight line QPT)
From (i) and (ii)
∠QRS = ∠SPT ...(iii)
Also, ∠RQS = ∠RPS ...(iv)
(Angle subtended by the same chord on the circle are equal)
And ∠RPS = ∠SPT
(PS bisects ∠RPT) ...(v)
From (iii), (iv) and (v)
∠QRS = ∠RQS
`=>` SQ = SR
APPEARS IN
संबंधित प्रश्न
ABCD is a cyclic quadrilateral in a circle with centre O. If ∠ADC = 130°; find ∠BAC.

In a cyclic quadrilateral ABCD, the diagonal AC bisects the angle BCD. Prove that the diagonal BD is parallel to the tangent to the circle at point A.
In the figure, ABCD is a cyclic quadrilateral with BC = CD. TC is tangent to the circle at point C and DC is produced to point G. If ∠BCG = 108° and O is the centre of the circle, find :
- angle BCT
- angle DOC

In following figure , O is the centre of the circle. If ∠ APB = 50° then find ∠ AOB and ∠ OAB.

In triangle ABC, AB = AC. A circle passing through B and c intersects the sides AB and AC at D and E respectively. Prove that DE || BC.
Prove that the angles bisectors of the angles formed by producing opposite sides of a cyclic quadrilateral (provided they are not parallel) intersect at right triangle.
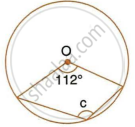
In the following figure, O is the centre of the circle. Find the values of a, b and c.
In the figure, ∠DBC = 58°. BD is a diameter of the circle. Calculate : ∠BDC
If O is the centre of the circle, find the value of x in each of the following figures
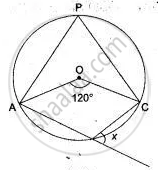
An exterior angle of a cyclic quadrilateral is congruent to the angle opposite to its adjacent interior angle, to prove the theorem complete the activity.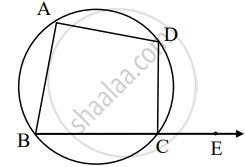
Given: ABCD is cyclic,
`square` is the exterior angle of ABCD
To prove: ∠DCE ≅ ∠BAD
Proof: `square` + ∠BCD = `square` .....[Angles in linear pair] (I)
ABCD is a cyclic.
`square` + ∠BAD = `square` ......[Theorem of cyclic quadrilateral] (II)
By (I) and (II)
∠DCE + ∠BCD = `square` + ∠BAD
∠DCE ≅ ∠BAD
