Advertisements
Advertisements
प्रश्न
In the given figure, SP is bisector of ∠RPT and PQRS is a cyclic quadrilateral. Prove that : SQ = SR.

उत्तर
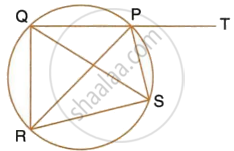
PQRS is a cyclic quadrilateral
∠QRS + ∠QPS = 180° ...(i)
(Pair of opposite angles in a cyclic quadrilateral are supplementary)
Also, ∠QPS + ∠SPT = 180° ...(ii)
(Straight line QPT)
From (i) and (ii)
∠QRS = ∠SPT ...(iii)
Also, ∠RQS = ∠RPS ...(iv)
(Angle subtended by the same chord on the circle are equal)
And ∠RPS = ∠SPT
(PS bisects ∠RPT) ...(v)
From (iii), (iv) and (v)
∠QRS = ∠RQS
`=>` SQ = SR
APPEARS IN
संबंधित प्रश्न
PQRS is a cyclic quadrilateral. Given ∠QPS = 73°, ∠PQS = 55° and ∠PSR = 82°, calculate:
1) ∠QRS
2) ∠RQS
3) ∠PRQ

ABCD is a cyclic quadrilateral in a circle with centre O. If ∠ADC = 130°; find ∠BAC.

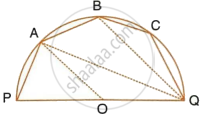
The given figure shows a semi-circle with centre O and diameter PQ. If PA = AB and ∠BCQ =140°; find measures of angles PAB and AQB. Also, show that AO is parallel to BQ.
Two circles intersect in points P and Q. A secant passing through P intersects the circles in A and B respectively. Tangents to the circles at A and B intersect at T. Prove that A, Q, B and T lie on a circle.
In the figure, O is the centre of the circle and the length of arc AB is twice the length of arc BC. If angle AOB = 108°, find: ∠ADB.
In the figure, ∠DBC = 58°. BD is a diameter of the circle. Calculate : ∠BEC
In the figure, ∠DBC = 58°. BD is a diameter of the circle. Calculate : ∠BAC
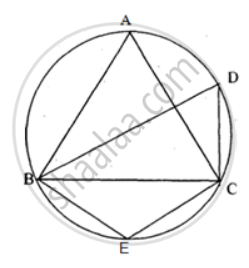
ABCD is a cyclic quadrilateral AB and DC are produced to meet in E. Prove that Δ EBC ∼ Δ EDA.
In the given below figure,
∠ BAD = 65°
∠ ABD = 70°
∠ BDC = 45°
Find: (i) ∠ BCD, (ii) ∠ ADB.
Hence show that AC is a diameter.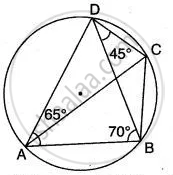
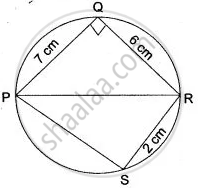
In the figure alongside PR is a diameter of the circle, PQ = 7 cm; QR = 6 cm and RS = 2 cm. Calculate the perimeter of the cyclic quadrilateral PQRS.