Advertisements
Advertisements
प्रश्न
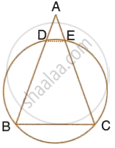
In the figure, ∠DBC = 58°. BD is a diameter of the circle. Calculate : ∠BEC
उत्तर
We know that the opposite angles of a cyclic quadrilateral are supplementary.
Thus, in cyclic quadrilateral BECD ,
∠ BEC + ∠ BDC = 180°
⇒ ∠ BEC + 32° = 180°
⇒ ∠ BEC = 180° - 32°
⇒ ∠ BEC = 148°
APPEARS IN
संबंधित प्रश्न
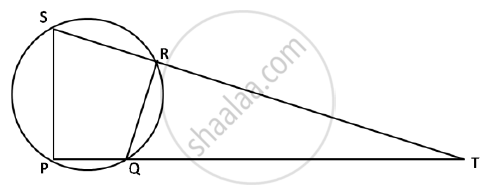
In the given figure PQRS is a cyclic quadrilateral PQ and SR produced meet at T
1) Prove ΔTPS ~ ΔTRQ.
2) Find SP if TP = 18 cm, RQ = 4 cm and TR = 6 cm
3) Find the area of quadrilateral PQRS if the area of ΔPTS = 27 cm2.
PQRS is a cyclic quadrilateral. Given ∠QPS = 73°, ∠PQS = 55° and ∠PSR = 82°, calculate:
1) ∠QRS
2) ∠RQS
3) ∠PRQ

In the figure, given below, find:
- ∠BCD,
- ∠ADC,
- ∠ABC.
Show steps of your working.

In the given figure, AB = AC. Prove that DECB is an isosceles trapezium.
In the figure, ABCD is a cyclic quadrilateral with BC = CD. TC is tangent to the circle at point C and DC is produced to point G. If ∠BCG = 108° and O is the centre of the circle, find :
- angle BCT
- angle DOC

ABCD is a cyclic quadrilateral in which BC is parallel to AD, angle ADC = 110° and angle BAC = 50°. Find angle DAC and angle DCA.
In following figure , Δ PQR is an isosceles teiangle with PQ = PR and m ∠ PQR = 35° .Find m ∠ QSR and ∠ QTR

In following figure.,ABCD is a cyclic quadrilateral . If ∠ BCD = 100° and ∠ ABD = 70° , find ∠ ADB.
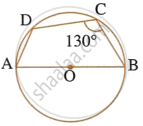
In the given figure, AB is the diameter of a circle with centre O.
∠BCD = 130°. Find:
- ∠DAB
- ∠DBA
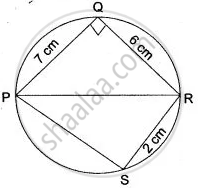
In the figure alongside PR is a diameter of the circle, PQ = 7 cm; QR = 6 cm and RS = 2 cm. Calculate the perimeter of the cyclic quadrilateral PQRS.