Advertisements
Advertisements
Question
In the figure, ∠DBC = 58°. BD is a diameter of the circle. Calculate : ∠BEC
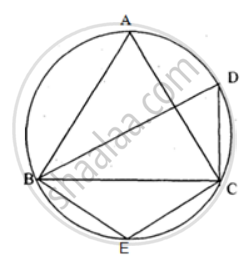
Solution
We know that the opposite angles of a cyclic quadrilateral are supplementary.
Thus, in cyclic quadrilateral BECD ,
∠ BEC + ∠ BDC = 180°
⇒ ∠ BEC + 32° = 180°
⇒ ∠ BEC = 180° - 32°
⇒ ∠ BEC = 148°
APPEARS IN
RELATED QUESTIONS
In the figure, ABCD is a cyclic quadrilateral with BC = CD. TC is tangent to the circle at point C and DC is produced to point G. If ∠BCG = 108° and O is the centre of the circle, find :
- angle BCT
- angle DOC

ABCD is a cyclic quadrilateral in which AB and DC on being produced, meet at P such that PA = PD. Prove that AD is parallel to BC.
In cyclic quadrilateral ABCD, ∠A = 3∠C and ∠D = 5∠B. Find the measure of each angle of the quadrilateral.
Prove that any four vertices of a regular pentagon are concylic (lie on the same circle).
In a cyclic quadrilateral ABCD , AB || CD and ∠ B = 65° , find the remaining angles.
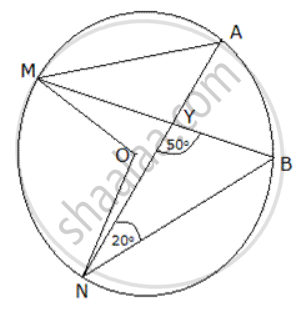
MABN are points on a drde having centre O. AN and MB cut at Y. If ∠ NYB = 50" and ∠ YNB = 200, find ∠ MAN and reflex angle MON.
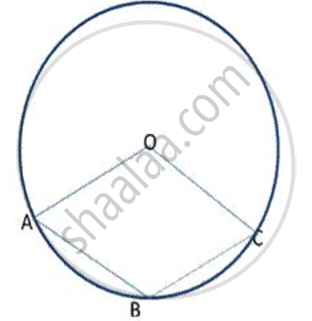
In fig., O is the centre of the circle and ∠ AOC = 1500. Find ∠ ABC.
The bisectors of the opposite angles A and C of a cydic quadrilateral ABCD intersect the cirde at the points E and F, respectively. Prove that EF is a diameter of the circle.
Prove that the angles bisectors of the angles formed by producing opposite sides of a cyclic quadrilateral (provided they are not parallel) intersect at right triangle.
ABCDE is a cyclic pentagon with centre of its circumcircle at point O such that AB = BC = CD and angle ABC=120°.
Calculate: ∠ BED.
